ক্রিশ্চিয়ান হাইজেনস এর জীবনী | Biography of Christiaan Huygens
ক্রিশ্চিয়ান হাইজেনস এর জীবনী | Biography of Christiaan Huygens

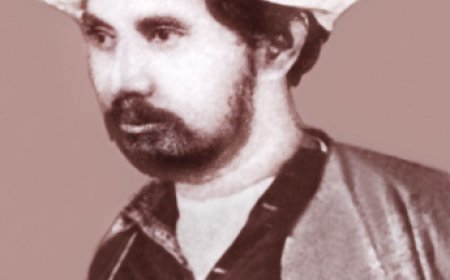
ক্রিশ্চিয়ান হাইজেনসের জীবনী, প্রফুল্ল বিজ্ঞানী
|
জন্ম |
14 April 1629 দ্য হগ, নেদারল্যান্ডস
|
|---|---|
|
মৃত্যু |
8 July 1695 (aged 66) নেদারল্যান্ডস
|
|
জাতীয়তা |
ওলন্দাজ |
|
মাতৃশিক্ষায়তন |
লিডেন বিশ্ববিদ্যালয় কলেজ অব অরেঞ্জ |
|
পরিচিতির কারণ |
টাইটান পেন্ডুলাম ঘড়ি হাইগেন-ফ্রেনেল নীতি তরঙ্গ তত্ত্ব |
|
বৈজ্ঞানিক কর্মজীবন |
|
|
কর্মক্ষেত্র |
পদার্থবিজ্ঞান গণিত জ্যোতির্বিদ্যা কালপরিমাপবিদ্যা |
|
প্রতিষ্ঠানসমূহ |
রয়েল সোসাইটি অব লন্ডন ফরাসি বিজ্ঞান একাডেমি |
|
ডক্টরাল উপদেষ্টা |
ফ্রাঞ্জ ফন শুটেন জন পেল |
|
যাদের দ্বারা প্রভাবিত হয়েছেন |
রেনে দেকার্ত ফ্রাঞ্জ ফন শুটেন |
|
যাদেরকে প্রভাবিত করেছেন |
গটফ্রিড ভিলহেলম লিবনিজ |
ক্রিশ্চিয়ান হাইগেনস ,
অথবা ক্রিশ্চিয়ান হাইগেনস , (জন্ম: ১৪ এপ্রিল, ১৬২৯, দ্য হেগ—মৃত্যু: ৮ জুলাই, ১৬৯৫, দ্য হেগ), ডাচ গণিতবিদ, জ্যোতির্বিদ এবং পদার্থবিদ। তিনিই প্রথম ঘড়ি নিয়ন্ত্রণের জন্য পেন্ডুলাম ব্যবহার করেন (১৬৫৬)। তিনি টেলিস্কোপ লেন্সগুলিকে পিষে এবং পালিশ করার একটি পদ্ধতি আবিষ্কার করেন এবং শনির বলয়ের প্রকৃত আকৃতি আবিষ্কার করার জন্য তিনি তার টেলিস্কোপ ব্যবহার করেন (১৬৫৯)।
তিনি গৌণ তরঙ্গ ফ্রন্টের নীতির উপর ভিত্তি করে প্রতিফলন এবং প্রতিসরণ ব্যাখ্যা করেন, যা এখন হাইগেনসের নীতি নামে পরিচিত। তিনি আলোর তরঙ্গ তত্ত্ব (১৬৭৮) তৈরি করেন এবং গতিবিদ্যা বিজ্ঞানেও অবদান রাখেন। ঘূর্ণায়মান বস্তুর উপর তাঁর গবেষণার ফলে পেন্ডুলামের দোলন এবং অভিন্ন বৃত্তাকার গতি সম্পর্কিত সমস্যার সমাধান হয়। তিনিই প্রথম ব্যক্তি যিনি মাধ্যাকর্ষণজনিত ত্বরণ নির্ধারণ করেন।
হাইগেনস প্রথম তার De Motu Corporum ex Percussione গ্রন্থে স্থিতিস্থাপক সংঘর্ষের সঠিক সূত্রগুলি সনাক্ত করেন , যা ১৬৫৬ সালে সম্পূর্ণ হয়েছিল কিন্তু মরণোত্তর ১৭০৩ সালে প্রকাশিত হয়েছিল। ১৬৫৯ সালে, হাইগেনস আইজ্যাক নিউটনের এক দশক আগে তার De vi Centrifuga গ্রন্থে কেন্দ্রাতিগ বলের জন্য ধ্রুপদী বলবিদ্যার সূত্রটি জ্যামিতিকভাবে বের করেছিলেন । আলোকবিদ্যায়, তিনি আলোর তরঙ্গ তত্ত্বের জন্য সর্বাধিক পরিচিত, যা তিনি তার Traité de la Lumière (১৬৯০) বইতে বর্ণনা করেছিলেন । আলোর তত্ত্বটি প্রাথমিকভাবে নিউটনের আলোক তত্ত্বের পক্ষে প্রত্যাখ্যান করা হয়েছিল , যতক্ষণ না অগাস্টিন-জিন ফ্রেসনেল ১৮২১ সালে আলোর রেক্টিলিনিয়ার প্রচার এবং বিবর্তনের প্রভাবের সম্পূর্ণ ব্যাখ্যা দেওয়ার জন্য হাইগেনসের নীতিকে অভিযোজিত করেন। আজ এই নীতিটি হাইগেনস-ফ্রেসনেল নীতি নামে পরিচিত ।
১৬৫৭ সালে হাইগেনস পেন্ডুলাম ঘড়ি আবিষ্কার করেন, যার পেটেন্ট তিনি একই বছর নেন। তাঁর হরোলজিক্যাল গবেষণার ফলে হোরোলজিয়াম অসিলেটরিয়াম (১৬৭৩) -এ পেন্ডুলামের একটি বিস্তৃত বিশ্লেষণ ঘটে , যা ১৭ শতকের বলবিদ্যার সবচেয়ে গুরুত্বপূর্ণ রচনাগুলির মধ্যে একটি হিসাবে বিবেচিত হয়। যদিও এতে ঘড়ির নকশার বর্ণনা রয়েছে, বইটির শিরভাগ অংশই পেন্ডুলাম গতি এবং বক্ররেখার তত্ত্বের বিশ্লেষণ । ১৬৫৫ সালে, হাইগেনস তার ভাই কনস্টান্টিজনের সাথে প্রতিসরণকারী টেলিস্কোপ তৈরির জন্য লেন্স পিষতে শুরু করেন । তিনি শনির বৃহত্তম চাঁদ, টাইটান আবিষ্কার করেন এবং শনির অদ্ভুত চেহারা ব্যাখ্যা করেন "একটি পাতলা, সমতল বলয়, কোথাও স্পর্শ না করা এবং গ্রহগ্রহণের দিকে ঝুঁকে থাকা" কারণে। ১৬৬২ সালে, তিনি বর্তমানে হুগেনিয়ান আইপিস নামে পরিচিত একটি টেলিস্কোপ তৈরি করেন, যা বিচ্ছুরণের পরিমাণ হ্রাস করার জন্য দুটি লেন্স সহ ।
একজন গণিতবিদ হিসেবে, হাইগেন্স বিবর্তনের তত্ত্ব তৈরি করেন এবং ভ্যান রেকেনিংহের স্পেলেন ভ্যান গ্লাক- এ সুযোগের খেলা এবং বিন্দুর সমস্যা নিয়ে লেখেন , যা ফ্রান্স ভ্যান স্কুটেন লুডো আলে (১৬৫৭) তে ডি রেটিওসিনিস নামে অনুবাদ এবং প্রকাশিত করেন । হাইগেন্স এবং অন্যান্যদের দ্বারা প্রত্যাশিত মানের ব্যবহার পরবর্তীতে জ্যাকব বার্নোলির সম্ভাব্যতা তত্ত্বের উপর কাজকে অনুপ্রাণিত করে ।
হাইগেনস প্রথমে গণিতে তার কাজের জন্য আন্তর্জাতিকভাবে পরিচিতি লাভ করেন, তিনি বেশ কয়েকটি গুরুত্বপূর্ণ ফলাফল প্রকাশ করেন যা অনেক ইউরোপীয় জিওমিটারের দৃষ্টি আকর্ষণ করে। হাইগেনসের প্রকাশিত রচনাগুলিতে আর্কিমিডিসের পছন্দের পদ্ধতি ছিল, যদিও তিনি তার ব্যক্তিগত নোটবুকগুলিতে ডেসকার্টসের বিশ্লেষণাত্মক জ্যামিতি এবং ফার্ম্যাটের অসীম কৌশলগুলি আরও ব্যাপকভাবে ব্যবহার করেছিলেন ।
প্রকাশিত রচনা
থিওরেমাটা ডি কোয়াড্রাটুরা
হাইগেন্সের প্রথম প্রকাশনা ছিল Theoremata de Quadratura Hyperboles, Ellipsis et Circuli ( অতিরিক্ত, উপবৃত্ত এবং বৃত্তের চতুর্ভুজের উপর উপপাদ্য ), যা ১৬৫১ সালে লিডেনে এলজেভিয়ার্স দ্বারা প্রকাশিত হয়েছিল । কাজের প্রথম অংশে অধিবৃত্ত, উপবৃত্ত এবং বৃত্তের ক্ষেত্র গণনার জন্য উপপাদ্য ছিল যা আর্কিমিডিসের শঙ্কু অংশের উপর কাজের সমান্তরাল ছিল, বিশেষ করে তার প্যারাবোলার চতুর্ভুজ । দ্বিতীয় অংশে গ্রেগোয়ার ডি সেন্ট-ভিনসেন্টের বৃত্ত চতুর্ভুজের উপর দাবির খণ্ডন অন্তর্ভুক্ত ছিল, যা তিনি আগে মার্সেনের সাথে আলোচনা করেছিলেন।
হাইগেনস দেখিয়েছিলেন যে যেকোনো হাইপারবোলা , উপবৃত্ত বা বৃত্তের একটি অংশের মাধ্যাকর্ষণ কেন্দ্র সরাসরি সেই অংশের ক্ষেত্রফলের সাথে সম্পর্কিত। এরপর তিনি শঙ্কু অংশে খোদাই করা ত্রিভুজ এবং সেই অংশগুলির জন্য মাধ্যাকর্ষণ কেন্দ্রের মধ্যে সম্পর্ক দেখাতে সক্ষম হন। সমস্ত শঙ্কু অংশকে অন্তর্ভুক্ত করার জন্য এই উপপাদ্যগুলিকে সাধারণীকরণ করে, নতুন ফলাফল তৈরি করার জন্য হাইগেনস ধ্রুপদী পদ্ধতিগুলি প্রসারিত করেছিলেন।
১৬৫০-এর দশকে চতুর্ভুজ এবং সংশোধন ছিল জীবন্ত বিষয় এবং মাইলনের মাধ্যমে, হাইগেন্স টমাস হবসকে ঘিরে বিতর্কে অংশগ্রহণ করেছিলেন । তার গাণিতিক অবদান তুলে ধরে তিনি আন্তর্জাতিক খ্যাতি অর্জন করেছিলেন।
ডি সার্কুলি ম্যাগনিটুডিন ইনভেনটা
হাইগেনসের পরবর্তী প্রকাশনা ছিল ডি সার্কুলি ম্যাগনিটুডিন ইনভেন্টা ( বৃত্তের মাত্রা সম্পর্কে নতুন অনুসন্ধান ), যা ১৬৫৪ সালে প্রকাশিত হয়েছিল। এই কাজে, হাইগেনস আর্কিমিডিসের বৃত্তের পরিমাপে প্রাপ্ত পরিধিযুক্ত এবং খোদাই করা বহুভুজের মধ্যে ব্যবধান সংকুচিত করতে সক্ষম হন, যা দেখায় যে পরিধির ব্যাস বা পাই ( π ) এর সাথে অনুপাত অবশ্যই সেই ব্যবধানের প্রথম তৃতীয়াংশে থাকা উচিত।
রিচার্ডসন এক্সট্রাপোলেশনের সমতুল্য একটি কৌশল ব্যবহার করে , হাইগেনস আর্কিমিডিসের পদ্ধতিতে ব্যবহৃত অসমতাগুলিকে সংক্ষিপ্ত করতে সক্ষম হন; এই ক্ষেত্রে, একটি প্যারাবোলার একটি অংশের মাধ্যাকর্ষণ কেন্দ্র ব্যবহার করে, তিনি একটি বৃত্তের একটি অংশের মাধ্যাকর্ষণ কেন্দ্রের আনুমানিক হিসাব করতে সক্ষম হন, যার ফলে বৃত্তের চতুর্ভুজের দ্রুত এবং নির্ভুল আনুমানিক হিসাব করা সম্ভব হয়। [ 75 ] এই উপপাদ্যগুলি থেকে, হাইগেনস π এর জন্য দুটি মানের সেট পেয়েছেন : প্রথমটি 3.1415926 এবং 3.1415927 এর মধ্যে, এবং দ্বিতীয়টি 3.1415926533 এবং 3.1415926538 এর মধ্যে।
হাইগেনস আরও দেখিয়েছেন যে, হাইপারবোলার ক্ষেত্রে , প্যারাবোলিক সেগমেন্টের সাথে একই আনুমানিকতা লগারিদম গণনা করার জন্য একটি দ্রুত এবং সহজ পদ্ধতি তৈরি করে । তিনি কাজের শেষে ইলাস্ট্রিয়াম কোরুন্ডাম প্রবলেমেটাম কনস্ট্রাকশনস ( কিছু বিখ্যাত সমস্যার নির্মাণ ) শিরোনামে ধ্রুপদী সমস্যার সমাধানের একটি সংগ্রহ যুক্ত করেছেন।
লুডো আলেয়েতে ডি রেটিওসিনিয়াস
১৬৫৫ সালে প্যারিস ভ্রমণের পর এবং কয়েক বছর আগে ফার্মাট, ব্লেইস প্যাসকেল এবং জিরার্ড ডেসার্গেসের কাজের মুখোমুখি হওয়ার পর হাইগেনস সুযোগের খেলায় আগ্রহী হয়ে ওঠেন। [ 78 ] তিনি অবশেষে লুডো আলেয়ে ( দৈবচয়নের খেলায় যুক্তি ) -এ ডি রেটিওসিনিস -এ সেই সময়ে সুযোগের খেলা সম্পর্কে গাণিতিক পদ্ধতির সবচেয়ে সুসংগত উপস্থাপনা প্রকাশ করেন । ফ্রান্স ভ্যান স্কুটেন মূল ডাচ পাণ্ডুলিপিটি ল্যাটিন ভাষায় অনুবাদ করেন এবং তার এক্সারসিটেশনাম ম্যাথেমেটিকারাম (১৬৫৭) বইয়ে প্রকাশ করেন ।

এই রচনাটিতে প্রাথমিক খেলা-তাত্ত্বিক ধারণা রয়েছে এবং বিশেষ করে পয়েন্টের সমস্যা নিয়ে আলোচনা করা হয়েছে । হাইগেনস প্যাসকেলের কাছ থেকে "ন্যায্য খেলা" এবং ন্যায়সঙ্গত চুক্তির ধারণা (অর্থাৎ, সম্ভাবনা সমান হলে সমান বিভাজন) গ্রহণ করেছিলেন এবং প্রত্যাশিত মূল্যবোধের একটি অ-মানক তত্ত্ব স্থাপনের জন্য যুক্তিটি প্রসারিত করেছিলেন। গণিতবিদদের কাছে এতদিন অপ্রাপ্য বলে মনে হওয়া সুযোগের ক্ষেত্রে বীজগণিত প্রয়োগে তার সাফল্য, ভিয়েট এবং ডেসকার্টেসের রচনায় পাওয়া প্রতীকী যুক্তির সাথে ইউক্লিডীয় সিন্থেটিক প্রমাণগুলিকে একত্রিত করার শক্তি প্রদর্শন করেছিল।
বইয়ের শেষে হাইগেনস পাঁচটি চ্যালেঞ্জিং সমস্যা অন্তর্ভুক্ত করেছেন যা পরবর্তী ষাট বছর ধরে সুযোগের খেলায় তাদের গাণিতিক দক্ষতা প্রদর্শন করতে ইচ্ছুক যে কারও জন্য আদর্শ পরীক্ষা হয়ে ওঠে। এই সমস্যাগুলি নিয়ে যারা কাজ করেছিলেন তাদের মধ্যে ছিলেন আব্রাহাম ডি মোইভর , জ্যাকব বার্নোলি, জোহানেস হুড , বারুচ স্পিনোজা এবং লিবনিজ।
অপ্রকাশিত কাজ
হাইগেনস এর আগে আর্কিমিডিসের " On Floating Bodies" বইয়ের আদলে " De Iis quae Liquido Supernatant" ( তরলের উপরে ভাসমান অংশ সম্পর্কে ) নামে একটি পাণ্ডুলিপি সম্পূর্ণ করেছিলেন । এটি ১৬৫০ সালের দিকে লেখা হয়েছিল এবং এতে তিনটি বই ছিল। যদিও তিনি সম্পূর্ণ কাজটি প্রতিক্রিয়ার জন্য ফ্রান্স ভ্যান স্কুটেনের কাছে পাঠিয়েছিলেন, শেষ পর্যন্ত হাইগেনস এটি প্রকাশ না করার সিদ্ধান্ত নেন এবং এক পর্যায়ে এটি পুড়িয়ে ফেলার পরামর্শ দেন। এখানে পাওয়া কিছু ফলাফল আঠারো এবং উনিশ শতক পর্যন্ত পুনরাবিষ্কৃত হয়নি।
টরিসেলির নীতির (অর্থাৎ, একটি সিস্টেমের বস্তুগুলি কেবল তখনই চলাচল করে যখন তাদের মাধ্যাকর্ষণ কেন্দ্র নেমে আসে) একটি চতুর প্রয়োগের মাধ্যমে গোলক এবং প্যারাবোলয়েডের স্থিতিশীলতার জন্য আর্কিমিডিসের সমাধানগুলি হাইগেনস প্রথমে পুনরায় আবিষ্কার করেন। এরপর তিনি সাধারণ উপপাদ্যটি প্রমাণ করেন যে, ভারসাম্যহীন ভাসমান বস্তুর জন্য, তার মাধ্যাকর্ষণ কেন্দ্র এবং তার নিমজ্জিত অংশের মধ্যে দূরত্ব সর্বনিম্ন। হাইগেনস এই উপপাদ্যটি ব্যবহার করে ভাসমান শঙ্কু , সমান্তরাল পাইপ এবং সিলিন্ডারের স্থিতিশীলতার জন্য মূল সমাধানে পৌঁছান , কিছু ক্ষেত্রে ঘূর্ণনের একটি পূর্ণ চক্রের মাধ্যমে। এইভাবে তার পদ্ধতি ভার্চুয়াল কাজের নীতির সমতুল্য ছিল । হাইগেনসই প্রথম স্বীকৃতি দেন যে, এই সমজাতীয় কঠিন পদার্থের জন্য, তাদের নির্দিষ্ট ওজন এবং তাদের আকৃতির অনুপাত হাইড্রোস্ট্যাটিক স্থিতিশীলতার অপরিহার্য পরামিতি ।
প্রাকৃতিক দর্শন
ডেসকার্টস এবং নিউটনের মধ্যে হাইগেনস ছিলেন শীর্ষস্থানীয় ইউরোপীয় প্রাকৃতিক দার্শনিক। তবে, তাঁর সমসাময়িক অনেকের বিপরীতে, হাইগেনসের গ্র্যান্ড তাত্ত্বিক বা দার্শনিক ব্যবস্থার প্রতি কোনও আগ্রহ ছিল না এবং সাধারণত অধিবিদ্যাগত বিষয়গুলি নিয়ে কাজ করা এড়িয়ে চলতেন (যদি চাপ দেওয়া হয়, তিনি তাঁর সময়ের কার্টেসিয়ান দর্শন মেনে চলতেন)। পরিবর্তে, হাইগেনস তাঁর পূর্বসূরীদের, যেমন গ্যালিলিওর, কাজকে প্রসারিত করার ক্ষেত্রে অসাধারণ ছিলেন, যাতে গাণিতিক বিশ্লেষণের জন্য উপযুক্ত অমীমাংসিত শারীরিক সমস্যার সমাধান বের করা যায়। বিশেষ করে, তিনি এমন ব্যাখ্যা খুঁজতেন যা দেহের মধ্যে যোগাযোগের উপর নির্ভর করে এবং দূরত্বে ক্রিয়া এড়িয়ে চলে ।
রবার্ট বয়েল এবং জ্যাক রোহল্টের সাথে মিল রেখে , হাইগেন্স তার প্যারিসের বছরগুলিতে একটি পরীক্ষামূলক-ভিত্তিক, যান্ত্রিক প্রাকৃতিক দর্শনের পক্ষে ছিলেন। ১৬৬১ সালে ইংল্যান্ডে তার প্রথম সফরের মধ্যেই, হাইগেন্স গ্রেশাম কলেজে একটি সভায় বয়েলের বায়ু পাম্প পরীক্ষা সম্পর্কে জানতে পেরেছিলেন । এর কিছুক্ষণ পরেই, তিনি বয়েলের পরীক্ষামূলক নকশা পুনর্মূল্যায়ন করেন এবং একটি নতুন অনুমান পরীক্ষা করার জন্য একাধিক পরীক্ষা-নিরীক্ষার ব্যবস্থা তৈরি করেন। এটি একটি দীর্ঘ প্রক্রিয়া প্রমাণিত হয়েছিল যা বেশ কয়েকটি পরীক্ষামূলক এবং তাত্ত্বিক সমস্যা উন্মোচন করেছিল এবং যা তিনি রয়্যাল সোসাইটির ফেলো হওয়ার সময় শেষ হয়েছিল। বয়েলের পরীক্ষা-নিরীক্ষার ফলাফলের পুনরাবৃত্তি অগোছালোভাবে অনুসরণ করা সত্ত্বেও , কার্টেসিয়ানদের অস্বীকৃতির বিরুদ্ধে হাইগেন্স শূন্যতা সম্পর্কে বয়েলের দৃষ্টিভঙ্গি গ্রহণ করতে শুরু করেছিলেন।
জন লকের উপর নিউটনের প্রভাবের মধ্যস্থতা করেছিলেন হাইগেন্স, যিনি লককে আশ্বস্ত করেছিলেন যে নিউটনের গণিত সঠিক, যার ফলে লক কর্পাসকুলার-যান্ত্রিক পদার্থবিদ্যা গ্রহণ করেছিলেন।
গতি, প্রভাব এবং মাধ্যাকর্ষণের সূত্র
ইলাস্টিক সংঘর্ষ
একই বছরে, হাইগেনস মঙ্গল গ্রহের একটি আগ্নেয়গিরির সমভূমি, সিরিটিস মেজর পর্যবেক্ষণ করতে সক্ষম হন । তিনি মঙ্গল গ্রহের দিনের দৈর্ঘ্য অনুমান করার জন্য বেশ কয়েক দিন ধরে এই বৈশিষ্ট্যের গতিবিধির বারবার পর্যবেক্ষণ ব্যবহার করেছিলেন, যা তিনি বেশ নির্ভুলভাবে 24 1/2 ঘন্টা করেছিলেন। এই পরিসংখ্যানটি মঙ্গল গ্রহের দিনের প্রকৃত দৈর্ঘ্য 24 ঘন্টা, 37 মিনিটের থেকে মাত্র কয়েক মিনিট কম।
প্ল্যানেটারিয়াম
জিন-ব্যাপটিস্ট কোলবার্টের প্ররোচনায়, হাইগেনস একটি যান্ত্রিক প্ল্যানেটারিয়াম নির্মাণের কাজ হাতে নেন যেখানে সূর্যের চারপাশে প্রদক্ষিণকারী সমস্ত গ্রহ এবং তাদের চাঁদগুলি প্রদর্শিত হতে পারে। হাইগেনস ১৬৮০ সালে তার নকশা সম্পন্ন করেন এবং পরের বছর তার ঘড়ি নির্মাতা জোহানেস ভ্যান সিউলেনকে এটি তৈরি করতে বলেন। যাইহোক, কলবার্ট এই সময়ের মধ্যে মারা যান এবং নতুন মন্ত্রী, ফ্রাঁসোয়া-মিশেল লে টেলিয়ার , হাইগেনসের চুক্তি নবায়ন না করার সিদ্ধান্ত নেওয়ায় হাইগেনস কখনও তার প্ল্যানেটারিয়াম ফরাসি একাডেমি অফ সায়েন্সেসের কাছে হস্তান্তর করতে পারেননি।
তার নকশায়, হাইগেনস অবিচ্ছিন্ন ভগ্নাংশের একটি উদ্ভাবনী ব্যবহার করে সর্বোত্তম যুক্তিসঙ্গত আনুমানিকতা খুঁজে বের করেছিলেন যার মাধ্যমে তিনি সঠিক সংখ্যক দাঁত সহ গিয়ারগুলি বেছে নিতে পারতেন। দুটি গিয়ারের মধ্যে অনুপাত দুটি গ্রহের কক্ষপথের সময়কাল নির্ধারণ করে। সূর্যের চারপাশে গ্রহগুলিকে ঘোরানোর জন্য, হাইগেনস একটি ঘড়ি-প্রণালী ব্যবহার করেছিলেন যা সময়ে সময়ে এগিয়ে এবং পিছনে যেতে পারে। হাইগেনস দাবি করেছিলেন যে তার প্ল্যানেটারিয়ামটি একই সময়ে ওলে রোমার দ্বারা নির্মিত অনুরূপ ডিভাইসের চেয়ে বেশি নির্ভুল ছিল , কিন্তু তার প্ল্যানেটারিয়ামের নকশাটি তার মৃত্যুর পরে ওপাসকুলা পোস্টহুমা (1703) প্রকাশিত হয়েছিল।
মৃত্যু:
হাইগেন্সের জীবনের শেষ পাঁচ বছর ছিল ক্রমাগত অসুস্থতা এবং ক্রমবর্ধমান একাকীত্ব ও বিষণ্ণতার অনুভূতি দ্বারা চিহ্নিত । তিনি ১৬৯৫ সালের মার্চ মাসে তার উইলে চূড়ান্ত সংশোধন করেন এবং একই বছরের শেষের দিকে অনেক কষ্টভোগের পর মারা যান।
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0