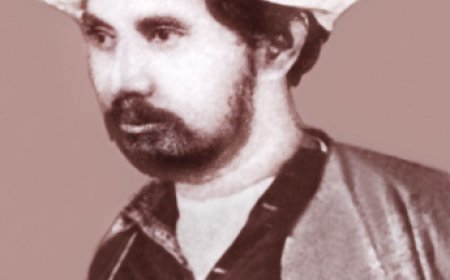
জন ভন নিউম্যান এর জীবনী | Biography of John von Neumann
জন ভন নিউম্যান এর জীবনী | Biography of John von Neumann

জন ভন নিউম্যান আর্কিটেকচার / ধারনা (John Von Neumann Architecture)
| জন্ম |
ন্যাউমান ইয়ানোশ লয়শ
(Neumann János Lajos) ২৮ ডিসেম্বর ১৯০৩ বুদাপেস্ট, অস্ট্রিয়া-হাঙ্গেরি
|
|---|---|
|
মৃত্যু |
ফেব্রুয়ারি ৮, ১৯৫৭ (বয়স ৫৩) ওয়াল্টা রিড আর্মি মেডিকেল সেন্টার
ওয়াশিংটন, ডি.সি. |
|
জাতীয়তা |
হাঙ্গেরীয় এবং মার্কিন |
|
মাতৃশিক্ষায়তন |
বিশ্ববিদ্যালয় ইটিএইচ জুরিখ |
|
পরিচিতির কারণ |
|
|
পুরস্কার |
বোশার স্মারক পুরস্কার (১৯৩৮), এনরিকো ফের্মি পুরস্কার (১৯৫৬) |
|
বৈজ্ঞানিক কর্মজীবন |
|
|
কর্মক্ষেত্র |
গণিত, পদার্থবিজ্ঞান, পরিসংখ্যান, অর্থনীতি |
| প্রতিষ্ঠানসমূহ | বার্লিনের হুমবোল্ট বিশ্ববিদ্যালয় প্রিন্সটন বিশ্ববিদ্যালয় ইন্সটিটিউট ফর অ্যাডভান্সড স্টাডি লস আলামোস ন্যাশনাল ল্যাবরেটরি |
|
ডক্টরাল উপদেষ্টা |
লিপিট ফেজার |
| অন্যান্য উচ্চশিক্ষায়তনিক উপদেষ্টা |
লাসল্লা রাত্জ |
|
ডক্টরেট শিক্ষার্থী |
ডোনাল্ড বি গিলিজ ইস্রায়েল হাল্পেরিন |
|
অন্যান্য উল্লেখযোগ্য শিক্ষার্থী |
পল রিচার্ড হ্যামস ক্লিফোর্ড হিউ ডাওকার |
জন ভন নিউমান
( /vɒn
ভন নিউমান গণিত ( গণিতের ভিত্তি, কার্যকরী বিশ্লেষণ, এরগোডিক তত্ত্ব, উপস্থাপনা তত্ত্ব, অপারেটর বীজগণিত, জ্যামিতি, টপোলজি এবং সংখ্যাসূচক বিশ্লেষণ ), পদার্থবিজ্ঞান ( কোয়ান্টাম মেকানিক্স, হাইড্রোডাইনামিক্স এবং কোয়ান্টাম স্ট্যাটিস্টিকাল মেকানিক্স ) অর্থনীতি ( গেম তত্ত্ব ), কম্পিউটিং ( ভন নিউম্যান আর্কিটেকচার, লিনিয়ার প্রোগ্রামিং, স্ব-প্রতিলিপি মেশিন, স্টোকাস্টিক কম্পিউটিং ) এবং পরিসংখ্যান সহ অনেক ক্ষেত্রে গুরুত্বপূর্ণ অবদান রেখেছিলেন। তিনি কার্যকরী বিশ্লেষণের বিকাশে কোয়ান্টাম মেকানিক্সের জন্য অপারেটর তত্ত্বের প্রয়োগের পথিকৃৎ এবং গেম তত্ত্বের বিকাশ এবং সেলুলার অটোমাতা, সার্বজনীন নির্মাতা এবং ডিজিটাল কম্পিউটারের ধারণাগুলির একজন মূল ব্যক্তিত্ব ছিলেন।
ভন নিউমান তার জীবনের প্রায় দেড় শতাধিক নিবন্ধ প্রকাশ করেছিলেন: গণিতে প্রায় ৬০, প্রয়োগিত গণিতে ৬০, পদার্থবিদ্যায় ২০ টি এবং বাকীগলো বিশেষ গাণিতিক বিষয় বা অ-গাণিতিক বিষয়ে। তাঁর শেষ রচনা, তিনি হাসপাতালে থাকাকালীন লিখিত একটি অসম্পূর্ণ পান্ডুলিপি, পরবর্তীকালে দ্য কম্পিউটার এবং ব্রেন নামে বই আকারে প্রকাশিত হয়েছিল।
স্ব-প্রতিরূপের কাঠামো সম্পর্কে তাঁর বিশ্লেষণ ডিএনএর কাঠামো আবিষ্কারের পূর্ববর্তী। তিনি ন্যাশনাল একাডেমি অফ সায়েন্সেস-এ জমা দেয়া তার জীবন সম্পর্কে তথ্যের সংক্ষিপ্ত তালিকায় তিনি লিখেছেন, "আমার যে কাজটি আমি সবচেয়ে জরুরি বলে বিবেচনা করি তা হ'ল কোয়ান্টাম মেকানিক্সের উপর, যা ১৯২৬ সালে গ্যাটিনজেন এবং পরে বার্লিনে ১৯২৭–১৯২৯ সালে বিকশিত হয়েছিল। এছাড়াও, বিভিন্ন ধরনের অপারেটর তত্ত্ব, বার্লিন ১৯৩০ এবং প্রিন্সটন ১৯৩৫-১৯৩৯; অরগোডিক উপপাদ্যে, প্রিন্সটন, ১৯৩১-১৯৩২ সম্পর্কে আমার কাজ।
দ্বিতীয় বিশ্বযুদ্ধের সময় ভন নিউমান ম্যানহাটন প্রকল্পে তাত্ত্বিক পদার্থবিজ্ঞানী এডওয়ার্ড টেলার, গণিতবিদ স্ট্যানিসলাউ উলাম এবং অন্যদের সাথে, থার্মোনিউক্লিয়াল বিক্রিয়ায় জড়িত পারমাণবিক পদার্থবিজ্ঞানের সমস্যা সমাধানের মূল পদক্ষেপ এবং হাইড্রোজেন বোমা নিয়ে কাজ করেছিলেন। তিনি প্রসারণ-ধরনের পারমাণবিক অস্ত্র ব্যবহৃত বিস্ফোরক লেন্সগুলির পিছনে গাণিতিক মডেলগুলি তৈরি করেছিলেন এবং উৎপন্ন বিস্ফোরক শক্তির পরিমাপ হিসাবে "কিলোটন" ( টিএনটি-এর) শব্দটি তৈরি করেছিলেন। যুদ্ধের পরে, তিনি মার্কিন যুক্তরাষ্ট্রের পারমাণবিক শক্তি কমিশনের সাধারণ উপদেষ্টা কমিটিতে দায়িত্ব পালন করেছিলেন এবং মার্কিন যুক্তরাষ্ট্রের বিমানবাহিনী, সেনাবাহিনীর ব্যালিস্টিক রিসার্চ ল্যাবরেটরি, সশস্ত্র বাহিনীর বিশেষ অস্ত্র প্রকল্প এবং লরেন্স লিভারমোর জাতীয় পরীক্ষাগার সহ সংস্থাগুলির জন্য পরামর্শ দেন। হাঙ্গেরীয় আমেরিকান হিসাবে যে সোভিয়েতরা পারমাণবিক শ্রেষ্ঠত্ব অর্জন করবে তা নিয়ে উদ্বিগ্ন হয়ে তিনি অস্ত্রের সীমাবদ্ধ করার জন্য পারস্পরিক আশ্বাসপ্রাপ্ত ধ্বংসের নীতিটি তৈরি ও প্রচার করেছিলেন।
পারিবারিক ইতিহাস
ক ধনী, সমৃদ্ধ এবং অ-পর্যবেক্ষক ইহুদি পরিবারে নিউম্যান জ্যানোস লাজোসের জন্ম হয়েছিল। হাঙ্গেরিয়ান ভাষায় পরিবারের নামটি প্রথমে আসে এবং তাঁর প্রদত্ত নামগুলি ইংরেজিতে জন লুইসের সমতুল্য।
ভন নিউমানের জন্ম হাঙ্গেরির বুদাপেস্টে, যা তখন অস্ট্রো-হাঙ্গেরিয়ান সাম্রাজ্যের অংশ ছিল। [৩][৪] [৫] তিনি তিন ভাইয়ের মধ্যে বড় ছিলেন; তাঁর দুই ছোট ভাইবোন হলেন মিহলি (ইংরেজি: মাইকেল ভন নিউমানান; ১৯০৭-১৯৮৯) এবং মিক্লাস (নিকোলাস ভন নিউমান, ১৯১১-২০১১)। তাঁর পিতা, নিউমান মিক্সা (ম্যাক্স ভন নিউমান, ১৮৭৩–১৯২৮) একজন ব্যাংকার ছিলেন, যিনি আইন বিষয়ে ডক্টরেট করেছিলেন। তিনি ১৮৮০ এর দশকের শেষে প্যাকস থেকে বুদাপেস্টে চলে এসেছিলেন।মিক্সার বাবা এবং দাদা দু'জনেরই উত্তর হাঙ্গেরির জেম্প্লেন কাউন্টি ওন্ডে (বর্তমানে সেজেরেন্স শহরের অংশ) জন্ম হয়েছিল। জন এর মা ছিলেন কান মার্গিট (ইংরেজি: মার্গারেট কানতার বাবা-মা ছিলেন জাকব কান এবং মাইসেলস পরিবারের কাতালিন মিজেলস। কান পরিবারের তিন প্রজন্ম বুদাপেস্টে কান-হেলারের অফিসের উপরে প্রশস্ত অ্যাপার্টমেন্টে বাস করত; ভন নিউমানের পরিবার উপরের তলায় একটি ১৮ কক্ষের অ্যাপার্টমেন্টে থাকত।
২০ ফেব্রুয়ারি, ১৯১৩ এ সম্রাট ফ্রানজ জোসেফ জন পিতাকে অস্ট্রো-হাঙ্গেরিয়ান সাম্রাজ্যে তাঁর কাজের জন্য হাঙ্গেরিয়ান আভিজাত্যের দিকে উন্নীত করেছিলেন। নিউমান পরিবার এভাবে বংশানুক্রমিকমার্গিটটাই অর্জন করেছিল, যার অর্থ "মার্গিট্টা" (আজকের মারঘিটা, রোমানিয়া )। শহরের সাথে পরিবারের কোনও যোগাযোগ ছিল না; মার্গারেটের প্রসঙ্গে এই আবেদনটি বেছে নেওয়া হয়েছিল, যেমনটি তাদের বেছে নেওয়া তিনটি মার্গুইরাইট চিত্রযুক্ত কোট। নিউমান জানোস মার্গিটটাই নিউউম্যান জানোস (জন নিউম্যান ডি মারজিটা) হয়েছিলেন, যা থেকে পরে তিনি জার্মান জোহান ফন নিউমানের হয়ে ওঠেন।
শিশু বয়সেই পরম বিস্ময়কর ব্যক্তি
ভন নিউমান একটি শিশু বয়স থেকেই পরম বিস্ময়কর ব্যক্তি ছিলেন। তিনি যখন ছয় বছর বয়সী ছিলেন, তখন তিনি মাথার মধ্যেই দুটি আট-অঙ্কের সংখ্যা ভাগ করতে পারতেন এবং প্রাচীন গ্রিক ভাষায় কথা বলতে পারেন। ছয় বছর বয়সী ভন নিউমান যখন তার মাকে লক্ষ্যহীনভাবে তাকিয়ে থাকতে দেখে তাকে জিজ্ঞাসা করেছিলেন, "আপনি কী হিসাব করছেন?"।
তারা যখন ছোট ছিল, পরিচারিকারা ভন নিউমন, তার ভাই এবং তার চাচাত ভাইদের শিক্ষা দিত। ম্যাক্স বিশ্বাস করতেন যে হাঙ্গেরিয়ান ছাড়াও অন্য ভাষার জ্ঞানও অপরিহার্য, তাই বাচ্চাদের ইংরেজি, ফরাসি, জার্মান এবং ইতালীয় ভাষাতে প্রশিক্ষণ দেওয়া হয়েছিল। আট বছর বয়সের মধ্যে ভন নিউউমন ডিফারেনশিয়াল এবং অবিচ্ছেদ্য ক্যালকুলাসের সাথে পরিচিত ছিলেন,তবে তিনি ইতিহাসে বিশেষ আগ্রহী ছিলেন। তিনি মাধ্যমে তার উপায় পড়া উইলহেম ওঙ্কেন এর আইনজেল্ডারস্টেলুঞ্জেনে এলজেমাইন গেসিচিট এর ৪৬টি ভলিয়ম পড়েছিলেন।ম্যাক্সের ক্রয় করা একটি অনুলিপি একটি ব্যক্তিগত লাইব্রেরিতে ছিল। অ্যাপার্টমেন্টের একটি কক্ষ একটি লাইব্রেরি এবং পাঠকক্ষে রূপান্তরিত হয়েছিল, যেখানে সিলিং থেকে মেঝে পর্যন্ত বইয়ের তাক ছিল।
ভন নিউমানান ১৯১৪ সালে লুথেরান ফ্যাসরি এভাঙ্গালিকাস জিমনজিয়ামে প্রবেশ করেছিলেন।ইউজিন উইগনার লুথেরান স্কুলে ভন নিউমানের এক বছর আগে ছিলেন এবং শীঘ্রই তাঁর বন্ধু হন। এটি বুদাপেস্টের অন্যতম সেরা স্কুল এবং এটি অভিজাতদের জন্য নকশাকৃত একটি উজ্জ্বল শিক্ষা ব্যবস্থার অংশ ছিল। হাঙ্গেরীয় সিস্টেমের অধীনে, শিশুরা তাদের সমস্ত শিক্ষা একটি জিমনেসিয়ামে পেয়েছিল। হাঙ্গেরিয়ান স্কুল ব্যবস্থা বৌদ্ধিক কৃতিত্বের জন্য খ্যাতিযুক্ত একটি প্রজন্ম তৈরি করেছিল, যার মধ্যে থিওডোর ভন কার্মেন (জন্ম ১৮৮১), জর্জ ডি হেভেসি (জন্ম ১৮৮৫), মাইকেল পোলানাই (জন্ম ১৮৯১), লে লে সিজিলার্ড (জন্ম ১৮৯৮), ডেনিস গ্যাবার (জন্ম ১৯০০), ইউজিন উইগনার (জন্ম ১৯০২), এডওয়ার্ড টেলার (জন্ম ১৯০৮), এবং পল এরদেস (জন্ম ১৯১৩)। সম্মিলিতভাবে, তারা কখনও কখনও " দ্যা মার্শিয়ান " নামে পরিচিত ছিল।
যদিও ম্যাক্স তার বয়সের উপযুক্ত গ্রেড স্তরে ভন নিউমানকে স্কুলে ভর্তি হওয়ার জন্য জোর দিয়েছিল, তবে তিনি যে অঞ্চলে ছিলেন সেখানে তাকে প্রাইভেট টিউটর নিয়োগের বিষয়ে সম্মত হন। ১৫ বছর বয়সে, তিনি বিশিষ্ট বিশ্লেষক গ্যাবার সেজিগের অধীনে উন্নত ক্যালকুলাস অধ্যয়ন শুরু করেছিলেন। প্রথম সাক্ষাতে, ছেলের গাণিতিক প্রতিভার সাথে সেজিগ এতটাই অবাক হয়েছিলেন যে তিনি অশ্রুসিক্ত হয়েছিলেন। ভন নিউমানের ক্যালকুলাসে যে সমস্যাগুলির উদ্ভব হয়েছিল তার কয়েকটির তাৎক্ষ্ণিক সমাধান তার বাবার স্টেশনারিতে আঁকা এবং এখনও বুদাপেস্টের ভন নিউমান আর্কাইভে প্রদর্শিত হচ্ছে। ১৯ বছর বয়সে ভন নিউমান দু'টি বড় অঙ্কের গাণিতিক গবেষণাপত্র প্রকাশ করেছিলেন, এর মধ্যে দ্বিতীয়টি অর্ডিনাল সংখ্যার আধুনিক সংজ্ঞা দেয় যা গেয়র্গ ক্যান্টরের সংজ্ঞাটিকে বহিষ্কার করে। জিমনেসিয়ামে তাঁর পড়াশোনা শেষে ভন নিউউমন গণিতের জন্য জাতীয় পুরস্কার এটভিস পুরস্কার জিতেছিলেন।
বিশ্ববিদ্যালয় পড়াশোনা
তাঁর বন্ধু থিওডোর ভন কার্মানের মতে, ভন নিউমানের বাবা চেয়েছিলেন যে জন তাকে শিল্পে অনুসরণ করে এবং এর মাধ্যমে তার সময় গণিতের চেয়ে আরও আর্থিকভাবে কার্যকর প্রচেষ্টাতে ব্যয় করতে পারে। আসলে, তার বাবা ভন কার্মন তার ছেলেকে গণিতকে তার প্রধান হিসাবে গ্রহণ না করার জন্য রাজি হবার জন্য বলেছিলেন। ভন নিউমান এবং তাঁর বাবা সিদ্ধান্ত নিয়েছিলেন যে সেরা ক্যারিয়ারের পথটি একজন রাসায়নিক প্রকৌশলী হওয়া। ভন নিউমানের এ বিষয়ে তেমন জ্ঞান ছিল না, তাই তাকে বার্লিন বিশ্ববিদ্যালয়ের রসায়নে দুই বছর, নন-ডিগ্রি কোর্স করার ব্যবস্থা করা হয়েছিল, এরপরে তিনি সম্মানজনক ইটিএইচ জুরিখের প্রবেশিকা পরীক্ষায় বসেন, যা তিনি ১৯৩২ সালের সেপ্টেম্বরে পাস করেছিলেন। একই সময়ে ভন নিউমানও বুদাপেস্টের পজমেনি পেটার বিশ্ববিদ্যালয়ে গণিতে পিএইচডি করতে যান। তাঁর থিসিসের জন্য, তিনি ক্যান্টরের সেট তত্ত্বটির একটি অডিওম্যাটাইজেশন তৈরি করতে বেছে নিয়েছিলেন। তিনি ১৯২৬ সালে ইটিএইচ জুরিখ থেকে রাসায়নিক প্রকৌশলী হিসাবে স্নাতক হন (যদিও উইগনার বলেছেন যে ভন নিউম্যান কখনও রসায়ন বিষয়ের সাথে খুব বেশি সংযুক্ত ছিলেন না), এবং পিএইচডি করার জন্য তাঁর শেষ পরীক্ষায় উত্তীর্ণ হন। গণিতে একই সাথে তার রাসায়নিক ইঞ্জিনিয়ারিং ডিগ্রির সাথে, যার মধ্যে উইগনার লিখেছিলেন, "সম্ভবত পিএইচডি থিসিস এবং পরীক্ষা একটি প্রশংসনীয় প্রচেষ্টা গঠন করেনি।" এরপরে তিনি রকিফেলার ফাউন্ডেশনের ডেভিড হিলবার্টের অধীনে গণিত অধ্যয়নের জন্য অনুদানে গুটিনজেন বিশ্ববিদ্যালয়ে যান।
গণিতে অবদান
ভন নিউম্যান প্রথমে সেট তত্ত্ব, বাস্তব চলকের ফাংশনসমূহের তত্ত্ব এবং গণিতের ভিত্তি-র ওপর আগ্রহী ছিলেন। তিনি সেট তত্ত্বের স্বতঃসিদ্ধায়নে (Axiomatization) অবদান রাখেন। একই সাথে তিনি কোয়ান্টাম বলবিজ্ঞানের গাণিতিক ভিত্তির ওপরেও আগ্রহী ছিলেন। কোয়ান্টাম বলবিজ্ঞান নিয়ে গবেষণা করতে গিয়েই তিনি হিলবার্ট জগতসমূহ অধ্যয়ন করেন এবং এগুলোর রিং অপারেটর সংক্রান্ত তত্ত্বের মৌলিক ফলাফলগুলো বের করেন। রিং অপারেটরের তত্ত্ব আরো ব্যাখ্যা করতে গিয়ে তিনি অবিচ্ছিন্ন জ্যামিতির ধারণা উপস্থাপন করেন। এছাড়া তিনি গ্রুপসমূহের প্রায় পর্যায়বৃত্ত ফাংশনসমূহের তত্ত্ব দেন এবং কমপ্যাক্ট গ্রুপ সংক্রান্ত হিলবার্টের ৫ম সমস্যার সমাধান করেন। কর্মজীবনের পরবর্তী পর্যায়ে তিনি ক্রীড়া তত্ত্ব (Game Theory) ও কম্পিউটার নকশাকরণে (Computer design) অবদান রাখেন। আধুনিক কম্পিউটারের মূল স্থাপত্যকে তার নামানুসারে ভন নিউম্যান স্থাপত্য বা Von neumann architecture বলা হয়ে থাকে।

এরগোডিক তত্ত্ব
১৯৩২ সালে প্রকাশিত একাধিক প্রবন্ধে, জন ফন নিউম্যান এরগোডিক তত্ত্বে মৌলিক অবদান রাখেন। এটি গণিতের একটি শাখা, যেখানে অপরিবর্তনশীল মান সহ গতিশীল ব্যবস্থার অবস্থা বিশ্লেষণ করা হয়। ১৯৩২ সালের এরগোডিক তত্ত্ব বিষয়ক প্রবন্ধগুলোর বিষয়ে পল হ্যালমস বলেছিলেন, "যদি ফন নিউম্যান জীবনে আর কিছু না-ও করতেন, কেবল এই প্রবন্ধগুলোই তাকে গণিতে অমর করে রাখার জন্য যথেষ্ট হতো।" এর আগেই তিনি অপারেটর তত্ত্ব নিয়ে কাজ করেছিলেন এবং এটি তার গড় এরগোডিক উপপাদ্যে গুরুত্বপূর্ণ ভূমিকা রেখেছিল।
এই উপপাদ্য এক-প্যারামিটার ইউনিটারি গ্রুপ
t → Vₜ
সম্পর্কে এবং বলে যে, হিলবার্ট স্পেসে প্রতিটি ভেক্টর φ-এর জন্য,
T→∞limT1∫0TVt(ϕ)dt
এই সীমাটি হিলবার্ট নর্ম দ্বারা সংজ্ঞায়িত মাত্রায় অস্তিত্ব রাখে এবং এটি এমন একটি ভেক্টর ψ-তে পরিণত হয় যাতে
Vₜ(ψ) = ψ
সব t-এর জন্য। এটি প্রথম প্রবন্ধে প্রমাণিত হয়। দ্বিতীয় প্রবন্ধে ফন নিউম্যান যুক্তি দেন যে তার এই ফলাফলগুলো বল্টজমানের এরগোডিক হাইপোথিসিস-এর সঙ্গে সম্পর্কিত শারীরবিজ্ঞানে প্রয়োগের জন্য যথেষ্ট। তবে তিনি এটাও বলেন যে সম্পূর্ণ এরগোডিসিটি তখনো অর্জিত হয়নি এবং ভবিষ্যতের জন্য এটিকে আলাদা করে চিহ্নিত করেন।
পরবর্তীতে সেই বছরেই তিনি আরও একটি প্রভাবশালী প্রবন্ধ প্রকাশ করেন, যা এরগোডিসিটির পদ্ধতিগত অধ্যয়ন শুরু করে। সেখানে তিনি একটি বিখ্যাত বিভাজন উপপাদ্য প্রমাণ করেন, যেখানে দেখানো হয় যে, রৈখিক বাস্তব রেখার এরগোডিক পরিমাপ-সংরক্ষণকারী ক্রিয়াগুলো হলো সেই মূল গঠন উপাদান, যেগুলো থেকে সমস্ত পরিমাপ-সংরক্ষণকারী ক্রিয়া তৈরি করা যায়। আরও কিছু গুরুত্বপূর্ণ উপপাদ্য তিনি সেখানে দিয়েছেন যেগুলোর গণিতের অন্যান্য শাখায় ব্যাপক প্রয়োগ রয়েছে, বিশেষত পল হ্যালমসের সঙ্গে করা যৌথ কাজেও।
পরিমাপ তত্ত্ব
পরিমাপ তত্ত্বে, n-মাত্রিক ইউক্লিডীয় স্থান ℝⁿ-এর জন্য "পরিমাপের সমস্যা" এইভাবে বলা যেতে পারে: “ℝⁿ-এর সব উপসেটের জন্য কি এমন একটি ধনাত্মক, স্বাভাবিকীকৃত, অপরিবর্তনশীল ও যোগযোগ্য সেট ফাংশন আছে?” ফেলিক্স হাউসডর্ফ ও স্টেফান বানাখ-এর কাজ দেখিয়েছে, n = 1 বা 2 হলে সমস্যাটির ধনাত্মক সমাধান আছে, কিন্তু উচ্চতর মাত্রার ক্ষেত্রে (বানাখ–টারস্কি প্যারাডক্সের কারণে) নেতিবাচক সমাধান মেলে। ফন নিউম্যান যুক্তি দেন, এই সমস্যা মূলত গোষ্ঠীতাত্ত্বিক প্রকৃতির: পরিমাপের অস্তিত্ব নির্ধারণ করা যায় সংশ্লিষ্ট রূপান্তর গোষ্ঠীর বৈশিষ্ট্য দেখে। দুই মাত্রা পর্যন্ত ইউক্লিডীয় গোষ্ঠী একটি সমাধানযোগ্য গোষ্ঠী, কিন্তু উচ্চতর মাত্রায় তা নয়—এই পার্থক্যই সমাধানকে নির্ধারণ করে।
১৯৪২ সালের আশেপাশে তিনি ডরোথি মাহারামকে দেখান কিভাবে প্রমাণ করতে হয় যে, প্রতিটি সম্পূর্ণ σ-সীমিত পরিমাপ স্থানে একটি গুণনীয় উত্তোলন (multiplicative lifting) রয়েছে। তিনি এটি নিজে প্রকাশ করেননি, কিন্তু মাহারাম পরে নিজেই একটি নতুন প্রমাণ দেন।
ফন নিউম্যানের বিভিন্ন প্রবন্ধে ব্যবহৃত যুক্তির পদ্ধতিগুলো তার ফলাফলের চেয়েও বেশি গুরুত্বপূর্ণ বলে ধরা হয়। অপারেটর অ্যালজেব্রায় মাত্রাতত্ত্বের (dimension theory) তার ভবিষ্যত গবেষণার প্রস্তুতি হিসেবে তিনি সীমিত বিভাজনের মাধ্যমে সমতুল্যতার ফলাফল ব্যবহার করেন এবং পরিমাপ সমস্যাকে ফাংশনের রূপে পুনঃসংজ্ঞায়িত করেন। তিনি হেয়ার-এর একটি প্রশ্নের উত্তরে একটি প্রবন্ধে প্রমাণ করেন যে, বাস্তব সংখ্যা রেখায় সব সীমিত ফাংশনের একটি অ্যালজেব্রা থাকা সম্ভব, যা প্রায় সর্বত্র সমান ফাংশনগুলোর শ্রেণীর প্রতিনিধিত্ব করে। তিনি স্টোন-এর সঙ্গে যৌথভাবে পরবর্তী প্রবন্ধগুলোতে এই সমস্যার আরও সাধারণীকরণ ও বীজগাণিতিক দিক নিয়ে আলোচনা করেন।
তিনি নতুন পদ্ধতিতে বিভিন্ন প্রকার পরিমাপের বিযুক্তকরণ (disintegration) প্রমাণ করেন এবং হেয়ার পরিমাপের এককত্বের নতুন একটি প্রমাণ দেন, যদিও এটি কেবল কম্প্যাক্ট গোষ্ঠীর জন্য কার্যকর। এই পদ্ধতি স্থানীয়ভাবে কম্প্যাক্ট গোষ্ঠীর ক্ষেত্রে প্রয়োগ করতে তাকে সম্পূর্ণ নতুন কৌশল আবিষ্কার করতে হয়। তিনি র্যাডন–নিকোডিম উপপাদ্যের একটি নতুন ও চতুর প্রমাণও দেন। ইনস্টিটিউট ফর অ্যাডভান্সড স্টাডিতে তার লেকচার নোটগুলো আমেরিকায় পরিমাপ তত্ত্বে গুরুত্বপূর্ণ উৎস হিসেবে ব্যবহৃত হতো এবং পরবর্তীতে তা প্রকাশিত হয়।
টপোলজিকাল গোষ্ঠী
পরিমাপ তত্ত্বে পূর্ববর্তী কাজ ব্যবহার করে, ফন নিউম্যান টপোলজিকাল গোষ্ঠী তত্ত্বেও অবদান রাখেন। তিনি গোষ্ঠীর উপর প্রায় পর্যায়িক ফাংশন নিয়ে একটি প্রবন্ধে বোহরের তত্ত্বকে যেকোনো গোষ্ঠীর জন্য প্রসারিত করেন। এরপর বোচনারের সঙ্গে যৌথভাবে তিনি একটি প্রবন্ধে এমন ফাংশনের তত্ত্ব উন্নত করেন, যেগুলো সংখ্যা নয়, বরং রৈখিক স্থানের উপাদান হিসেবে মান নেয়।
১৯৩৩ সালে একটি প্রবন্ধে তিনি হেয়ার পরিমাপ ব্যবহার করে হিলবার্টের পঞ্চম সমস্যার সমাধান দেন, কম্প্যাক্ট গোষ্ঠীর ক্ষেত্রে। এর মূল ধারণা কয়েক বছর আগেই এসেছিল, যখন তিনি প্রকাশ করেছিলেন যে সাধারণ লিনিয়ার গোষ্ঠীর বন্ধ গোষ্ঠীগুলো আসলে লাই গোষ্ঠী। পরে কার্তান এই তত্ত্বকে যেকোনো লাই গোষ্ঠীতে সম্প্রসারিত করেন।
কার্যকরী বিশ্লেষণ (Functional Analysis)
ফন নিউম্যান প্রথম ব্যক্তি যিনি বিমূর্ত হিলবার্ট স্পেসকে স্বতঃসিদ্ধভাবে সংজ্ঞায়িত করেন। এটি একটি জটিল ভেক্টর স্থান, যেখানে একটি হারমিশিয়ান স্কেলার গুণফল রয়েছে এবং সংশ্লিষ্ট নর্মটি সম্পূর্ণ ও বিভাজ্য। একই প্রবন্ধে তিনি ক্যাউচি–শোয়ার্জ অসমতার সাধারণ রূপ প্রমাণ করেন, যা আগে শুধুমাত্র নির্দিষ্ট উদাহরণে জানা ছিল।
১৯২৯ থেকে ১৯৩২ পর্যন্ত তিনটি গুরুত্বপূর্ণ প্রবন্ধে তিনি হিলবার্ট স্পেসে অপারেটরের স্পেকট্রাল তত্ত্ব উন্নয়ন করেন। এই কাজ culminate করে তার বিখ্যাত বই Mathematical Foundations of Quantum Mechanics-এ, যা স্টোন ও বানাখ-এর সমসাময়িক বইগুলোর সঙ্গে মিলে হিলবার্ট স্পেস তত্ত্বের প্রথম মনোগ্রাফ হিসেবে বিবেচিত হয়।
তিনি সিকোয়েন্স দিয়ে দুর্বল টপোলজি গঠন করা যায় না জেনে, প্রথমবারের মতো লোকালিভাল কনভেক্স স্পেস ও টপোলজিকাল ভেক্টর স্পেস সংজ্ঞায়িত করেন। হাউসডর্ফের ইউক্লিডীয় ধারণা থেকে তিনি নতুন টপোলজিকাল ধারণা হিলবার্ট স্পেসে প্রয়োগ করেন, যার মধ্যে সীমাবদ্ধতা (boundedness) ও সর্বাঙ্গীন সীমাবদ্ধতা (total boundedness) আজও ব্যবহৃত হয়। কুয়ান্টাম মেকানিক্সে প্রয়োগের প্রয়োজনেই তার এই গবেষণাগুলো চালিত হয়।
এই কাজগুলোতে তার আরও কিছু গুরুত্বপূর্ণ অবদান হলো:
-
স্বাভাবিক অপারেটরের জন্য পূর্ণ স্পেকট্রাল বিশ্লেষণ।
-
ধনাত্মক অপারেটরের ট্রেস-এর বিমূর্ত উপস্থাপনা।
-
হিলবার্টের স্পেকট্রাল উপপাদ্যের সাধারণায়ন।
-
হারমিশিয়ান ও সেল্ফ-অ্যাডজয়েন্ট অপারেটরের মধ্যকার পার্থক্য চিহ্নিতকরণ।
তিনি দেখান যে, স্পেকট্রাল তত্ত্বে ব্যবহৃত অসীম ম্যাট্রিক্স প্রকৃত হারমিশিয়ান অপারেটরকে যথাযথভাবে উপস্থাপন করতে পারে না। অপারেটর তত্ত্বে তার এই কাজ ফন নিউম্যান অ্যালজেব্রা এবং আরও সাধারণভাবে অপারেটর অ্যালজেব্রা বিষয়ক বিশ্লেষণের পথ উন্মোচন করে, যা তার সবচেয়ে গভীর তাত্ত্বিক অবদান হিসেবে বিবেচিত।
মৃত্যু:
অবশেষে ১৯৫৭ সালের ৮ ফেব্রুয়ারি ক্যান্সারে আক্রান্ত হয়ে ওয়াশিংটন ডিসির ওয়াল্টার রিড আর্মি মেডিকেল সেন্টারে সামরিক নিরাপত্তার অধীনে মাত্র ৫৩ বছর বয়সে জগদ্বিখ্যাত গণিতবিদ জন ভন নিউম্যানের মৃত্যু হয়।
soruse : wikipedia .. en
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0