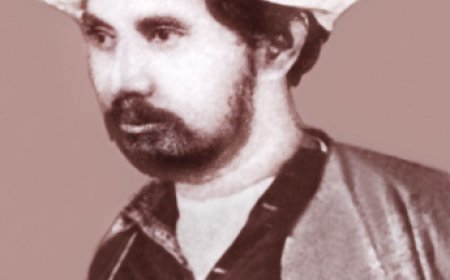
গ্রিগোরি পেরেলমান এর জীবনী | Biography of Grigori Perelman
গ্রিগোরি পেরেলমান এর জীবনী | Biography of Grigori Perelman

গ্রিগরি পেরেলম্যান: সিংহাসন ছেড়ে বনবাসে
|
পুরো নাম
|
গ্রিগোরি ইয়াকোভলেভিচ পেরেলম্যান |
|
জন্ম
|
১৩ জুন ১৯৬৬ (বয়স ৫৮) |
|
জন্মস্থান
|
লেনিনগ্রাদ, সোভিয়েত ইউনিয়ন (বর্তমানে সেন্ট পিটার্সবার্গ, রাশিয়া) |
|
শিক্ষা
|
লেনিনগ্রাদ স্টেট ইউনিভার্সিটি (পিএইচ.ডি.) |
|
থিসিস |
ইউক্লিডীয় স্থানে স্যাডল পৃষ্ঠসমূহ (Saddle Surfaces in Euclidean Spaces, ১৯৯০) |
|
তত্ত্বাবধায়ক
|
আলেক্সান্ডর আলেক্সান্দ্রভ, ইউরি বুরাগো |
|
পরিচিতি |
- সোল অনুমান প্রমাণ |
|
ক্ষেত্র
|
বিভাজন জ্যামিতি, জ্যামিতিক বিশ্লেষণ, জ্যামিতিক টপোলজি |
|
কর্মস্থল |
- স্টেকলভ গণিত ইনস্টিটিউট (PDMI) |
|
পুরস্কার |
- সেন্ট পিটার্সবার্গ গণিত সমিতি পুরস্কার (১৯৯১) |
জীবনী:
জ্যামিতিতে তাঁর অবদানের জন্য গ্রিগরি পেরেলম্যানকে ২০০৬ সালের অগস্ট মাসে গণিতের সর্বোচ্চ পুরস্কার ‘ফিল্ড মেডেল’ দেওয়ার কথা ঘোষণা করে ইন্টারন্যাশনাল কংগ্রেস অব ম্যাথামেটিক্স। লিখছেন অয়ন মুখোপাধ্যায়২০০০ সালের শুরুর দিক। ‘ক্লে ম্যাথামেটিকস ইনস্টিটিউড’ সাতটি গুরুত্বপূর্ণ গণিতের সমস্যা সমাধানের চ্যালেঞ্জ ছুঁড়ে দেয় পৃথিবীবাসীর উদ্দেশ্যে।
গ্রিগোরি ইয়াকোভলেভিচ পেরেলমান
(রাশিয়ান: Григорий Яковлевич Перельман; জন্ম ১৩ জুন ১৯৬৬) একজন রাশিয়ান গণিতবিদ এবং জ্যামিতিবিদ যিনি জ্যামিতিক বিশ্লেষণ, রিম্যানীয় জ্যামিতি এবং জ্যামিতিক টপোলজির ক্ষেত্রে গুরুত্বপূর্ণ অবদানের জন্য পরিচিত। ২০০৫ সালে তিনি স্টেকলভ ইনস্টিটিউট অব ম্যাথেমেটিকস থেকে পদত্যাগ করেন এবং ২০০৬ সালে পেশাদার গণিত ত্যাগ করার কথা ঘোষণা করেন, কারণ তিনি গণিত জগতে নৈতিক মান নিয়ে হতাশ ছিলেন। তিনি সেন্ট পিটার্সবার্গে নিভৃতে বসবাস করছেন এবং ২০০৬ সাল থেকে কোনো সাক্ষাৎকারে অংশগ্রহণ করেননি।
১৯৯০-এর দশকে, ইউরি বুরাগো, মিখাইল গ্রোমভ এবং আন্তন পেত্রুনিনের সাথে আংশিক সহযোগিতায়, তিনি আলেক্সান্দ্রভ স্পেস নিয়ে গবেষণায় অবদান রাখেন। ১৯৯৪ সালে, তিনি রিম্যানীয় জ্যামিতির একটি গুরুত্বপূর্ণ উন্মুক্ত সমস্যা "সোল কনজেকচার" প্রমাণ করেন, যা ২০ বছর ধরে অমীমাংসিত ছিল। ২০০২ এবং ২০০৩ সালে, তিনি রিচি ফ্লো বিশ্লেষণে নতুন কৌশল উদ্ভাবন করেন এবং পোয়াঙ্কারে কনজেকচার ও থার্স্টনের জ্যামিতিকরণ কনজেকচার প্রমাণ করেন। পোয়াঙ্কারে কনজেকচার শতাব্দীর পর শতাব্দী ধরে গণিতের একটি সবচেয়ে বিখ্যাত উন্মুক্ত সমস্যা ছিল। পরবর্তী কয়েক বছরে বিভিন্ন গবেষক তার কাজের পূর্ণ বিশ্লেষণ ও ব্যাখ্যা দেন।
আগস্ট ২০০৬-এ, পেরেলমানকে ফিল্ডস মেডেল প্রস্তাব করা হয় "জ্যামিতিতে তার অবদান এবং রিচি ফ্লো-এর বিশ্লেষণাত্মক ও জ্যামিতিক গঠন নিয়ে তার যুগান্তকারী দৃষ্টিভঙ্গির জন্য", কিন্তু তিনি এই পুরস্কার প্রত্যাখ্যান করেন, এই বলে:
"আমি টাকা বা খ্যাতির প্রতি আগ্রহী নই; আমি চিড়িয়াখানার জন্তুর মতো প্রদর্শনীতে থাকতে চাই না।"
২২ ডিসেম্বর ২০০৬-এ, সায়েন্স সাময়িকী পোয়াঙ্কারে কনজেকচারের প্রমাণকে বছরের সবচেয়ে বড় বৈজ্ঞানিক অগ্রগতি (Breakthrough of the Year) হিসেবে স্বীকৃতি দেয় — এটি ছিল গণিতের ক্ষেত্রে প্রথমবারের মতো এধরনের স্বীকৃতি।
১৮ মার্চ ২০১০-এ ঘোষণা করা হয় যে পেরেলমান ক্লে মিলেনিয়াম প্রাইজ পাওয়ার যোগ্যতা অর্জন করেছেন, পোয়াঙ্কারে কনজেকচার প্রমাণের জন্য। কিন্তু ১ জুলাই ২০১০-এ, তিনি এক মিলিয়ন ডলারের এই পুরস্কার প্রত্যাখ্যান করেন, এই বলে যে ক্লে ইনস্টিটিউটের বোর্ডের সিদ্ধান্ত তিনি ন্যায্য মনে করেন না, কারণ রিচার্ড এস. হ্যামিল্টনের অবদানও এই সমস্যার সমাধানে সমান গুরুত্বপূর্ণ ছিল, যিনি রিচি ফ্লো পদ্ধতির পথপ্রদর্শক ছিলেন। এর আগেও, ১৯৯৬ সালে তিনি ইউরোপিয়ান ম্যাথেমেটিক্যাল সোসাইটির সম্মানজনক পুরস্কার প্রত্যাখ্যান করেছিলেন।
প্রারম্ভিক জীবন ও শিক্ষা
গ্রিগোরি ইয়াকোভলেভিচ পেরেলমান জন্মগ্রহণ করেন লেনিনগ্রাদ, সোভিয়েত ইউনিয়নে (বর্তমানে সেন্ট পিটার্সবার্গ, রাশিয়া) ১৩ জুন ১৯৬৬ সালে, ইহুদি পরিবারে। তার বাবা ইয়াকভ (বর্তমানে ইসরায়েলে বসবাস করছেন) এবং মা লিউবোভ (যিনি এখনও সেন্ট পিটার্সবার্গে পেরেলমানের সাথে থাকেন)। পেরেলমানের মা লিউবোভ তার গণিতে স্নাতকোত্তর পড়া ছেড়ে ছেলের দেখাশোনায় মনোনিবেশ করেন। মাত্র ১০ বছর বয়সে তার গণিত প্রতিভা স্পষ্ট হয়ে ওঠে এবং তার মা তাকে সের্গেই রুকশিনের বিকেল-বেলার গণিত প্রশিক্ষণ কেন্দ্রে ভর্তি করান।
তার গণিত শিক্ষা লেনিনগ্রাদ সেকেন্ডারি স্কুল ২৩৯-এ চলতে থাকে, যা গণিত ও পদার্থবিদ্যায় বিশেষায়িত একটি বিদ্যালয়। পেরেলমান সব বিষয়েই অসাধারণ দক্ষ ছিলেন, তবে শারীরিক শিক্ষায় পিছিয়ে ছিলেন। ১৯৮২ সালে, ১৬ বছর বয়সে, তিনি সোভিয়েত দলের একজন সদস্য হিসেবে আন্তর্জাতিক গণিত অলিম্পিয়াডে অংশ নিয়ে স্বর্ণপদক অর্জন করেন, এবং পূর্ণ নম্বর পান।
তিনি পরীক্ষায় না বসেই লেনিনগ্রাদ স্টেট ইউনিভার্সিটির স্কুল অফ ম্যাথেমেটিক্স অ্যান্ড মেকানিক্সে (স্থানীয়ভাবে "মাতমেখ" নামে পরিচিত) ভর্তি হন।
১৯৯০ সালে পিএইচডি সম্পন্ন করার পর তিনি সোভিয়েত একাডেমি অব সায়েন্সেস-এর স্টেকলভ ইনস্টিটিউটের লেনিনগ্রাদ বিভাগে গবেষণা শুরু করেন, যেখানে তার উপদেষ্টা ছিলেন আলেক্সান্দর আলেক্সান্দ্রভ এবং ইউরি বুরাগো। ১৯৮০-এর শেষ ও ১৯৯০-এর শুরুর দিকে, জ্যামিতিবিদ মিখাইল গ্রোমভের সুপারিশে তিনি যুক্তরাষ্ট্রের বিভিন্ন বিশ্ববিদ্যালয়ে গবেষণা পদ পান। ১৯৯১ সালে, তিনি "আলেক্সান্দ্রভ স্পেস"-এ গবেষণার জন্য সেন্ট পিটার্সবার্গ ম্যাথেমেটিক্যাল সোসাইটি'র "ইয়ং ম্যাথেমেটিশিয়ান প্রাইজ" লাভ করেন।
১৯৯২ সালে তিনি নিউ ইয়র্ক ইউনিভার্সিটির কুরান্ট ইনস্টিটিউটে এক সেমিস্টার কাটান এবং রিচি কার্ভেচারের নিম্ন সীমা বিশিষ্ট ম্যানিফোল্ড নিয়ে কাজ শুরু করেন। এরপর ১৯৯৩ সালে ক্যালিফোর্নিয়া বিশ্ববিদ্যালয়, বার্কলেতে দু’বছরের জন্য মিলার রিসার্চ ফেলোশিপ গ্রহণ করেন। ১৯৯৪ সালে সোল কনজেকচার প্রমাণ করার পর, তাকে প্রিন্সটন এবং স্ট্যানফোর্ডসহ যুক্তরাষ্ট্রের বহু শীর্ষস্থানীয় বিশ্ববিদ্যালয় থেকে চাকরির প্রস্তাব দেওয়া হয়, কিন্তু তিনি সব প্রত্যাখ্যান করে ১৯৯৫ সালের গ্রীষ্মে সেন্ট পিটার্সবার্গে স্টেকলভ ইনস্টিটিউটে একটি গবেষণামূলক পদে ফিরে যান।
প্রাথমিক গবেষণা
উত্তল জ্যামিতি (Convex Geometry)
স্নাতক পর্যায়ে গ্রিগোরি পেরেলমান উত্তল জ্যামিতি (convex geometry) নিয়ে কাজ করেন। তার প্রথম প্রকাশিত প্রবন্ধে উত্তল বহুপৃষ্ঠকের (convex polyhedra) ছেদ থেকে উদ্ভূত যৌগিক কাঠামো (combinatorial structures) বিশ্লেষণ করা হয়। আই. ভি. পোলিকানোভার সঙ্গে যৌথভাবে তিনি হেলির উপপাদ্যের (Helly's Theorem) একটি পরিমাপক তাত্ত্বিক রূপ (measure-theoretic formulation) উপস্থাপন করেন। ১৯৮৭ সালে, যখন তিনি স্নাতকোত্তর পড়া শুরু করেন, তিনি একটি প্রবন্ধ প্রকাশ করেন যেখানে বৃত্তাকারে বেষ্টিত নলাকার আকৃতি (circumscribed cylinders) ও অভ্যন্তরে অঙ্কিত গোলকের (inscribed spheres) আকার নিয়ন্ত্রণ নিয়ে আলোচনা করেন।
নেতিবাচক বক্রতার অতিপৃষ্ঠ (Negatively Curved Hypersurfaces)
নেতিবাচক বক্রতার পৃষ্ঠ (surfaces of negative curvature) ছিল পেরেলমানের স্নাতকোত্তর গবেষণার বিষয়। তার প্রথম সাফল্য ছিল—তিন-মাত্রিক ইউক্লিডীয় স্থানে নেতিবাচক-বক্রতাযুক্ত বহুপৃষ্ঠের গঠন নির্ধারণের সম্ভাবনা প্রমাণ করা। তিনি দেখান যে, সমতলে এমন যেকোনো পূর্ণাঙ্গ মেট্রিক (complete metric) ধারাবাহিকভাবে একটি বহুপৃষ্ঠ আকারে প্রতিস্থাপন (immersed) করা সম্ভব।
পরবর্তীতে তিনি একটি চতুর্মাত্রিক ইউক্লিডীয় স্থানে একটি মসৃণ অতিপৃষ্ঠ (smooth hypersurface) নির্মাণ করেন, যা পূর্ণাঙ্গ এবং যার গাউস বক্রতা (Gaussian curvature) নেতিবাচক ও শূন্য থেকে দূরে। পূর্বে এমন কিছু উদাহরণ জানা ছিল, কিন্তু পেরেলমানের উদাহরণটি ছিল প্রথম যেটি "স্যাডল" বৈশিষ্ট্য প্রদর্শন করে—অর্থাৎ যেকোনো স্থানীয়ভাবে কঠোর সহায়ক অতিপৃষ্ঠ (strictly supporting hyperplanes) না থাকার বৈশিষ্ট্য। তার এই নির্মাণ নিকোলাই ইফিমভের (Nikolai Efimov) একটি পরিচিত উপপাদ্যকে উচ্চ মাত্রায় সম্প্রসারণের পথে আরেকটি বাধা হিসেবে বিবেচিত হয়।
আলেক্সান্দ্রভ স্পেস (Alexandrov Spaces)
পেরেলমানের গণিত সাহিত্যে প্রথম বড় প্রভাব ফেলে তার আলেক্সান্দ্রভ স্পেস (Alexandrov Spaces) বিষয়ক গবেষণা, যার ধারণা ১৯৫০-এর দশক থেকে চলে আসছে। ইউরি বুরাগো ও মিখাইল গ্রোমভের সঙ্গে একটি বিখ্যাত প্রবন্ধে, তিনি আধুনিকভাবে এই ক্ষেত্রের ভিত্তি স্থাপন করেন, যেখানে গ্রোমভ–হাউসডরফ একত্রীকরণ (Gromov–Hausdorff convergence) একটি সাংগঠনিক নীতিরূপে ব্যবহৃত হয়।
পরবর্তী এক অপ্রকাশিত প্রবন্ধে তিনি তার "স্থিতিশীলতা উপপাদ্য" (stability theorem) প্রমাণ করেন, যেখানে বলা হয়: নির্দিষ্ট বক্রতা সীমাযুক্ত সব আলেক্সান্দ্রভ স্পেসের মাঝে, একটি নির্দিষ্ট সংক্ষিপ্ত বলয় (metric ball)-এর সকল স্পেস একে অপরের সাথে হোমিওমরফিক (homeomorphic)। ভিটালি কাপোভিচ পেরেলমানের প্রবন্ধটিকে "অত্যন্ত কঠিন" হিসেবে উল্লেখ করলেও, পরে একটি বিস্তারিত সংস্করণ লেখেন।
পেরেলমান আলেক্সান্দ্রভ স্পেসে মরস তত্ত্বের (Morse theory) একটি সংস্করণ তৈরি করেন। যদিও আলেক্সান্দ্রভ স্পেস মসৃণ নয়, তবুও তিনি ও আন্তন পেত্রুনিন কিছু নির্দিষ্ট ফাংশনের গ্রেডিয়েন্ট ফ্লো নিয়ে কাজ করেন। তারা "চূড়ান্ত উপসেট" (extremal subset) নামক একটি ধারণা চালু করেন এবং দেখান যে এই উপসেটগুলোর অভ্যন্তরভাগ আলেক্সান্দ্রভ স্পেসকে টপোলজিক্যাল ম্যানিফোল্ড দ্বারা স্তরায়িত করে। পরবর্তী অপ্রকাশিত গবেষণায়, পেরেলমান আলেক্সান্দ্রভ স্পেসে DC ফাংশন (difference of concave functions) নিয়ে কাজ করেন এবং দেখান যে নিয়মিত বিন্দুগুলোর গঠন একটি DC মডেলযুক্ত ম্যানিফোল্ডের মত।
এই গবেষণার জন্য তিনি ১৯৯৪ সালে আন্তর্জাতিক গণিত সম্মেলনে আমন্ত্রিত বক্তৃতা দেওয়ার সুযোগ পান।
তুলনামূলক জ্যামিতি (Comparison Geometry)
১৯৭২ সালে, জেফ চিগার এবং ডেটলেফ গ্রোমল "সোল থিওরেম" প্রমাণ করেন। এতে বলা হয় যে, যেকোনো পূর্ণ রিম্যানীয় মেট্রিক যেটির সেকশনাল কার্ভেচার অ-নেতিবাচক, তার একটি সঙ্কুচিত উপ-ম্যানিফোল্ড (soul) থাকে যার স্বাভাবিক বান্ডিল (normal bundle) মূল স্পেসের সাথে ডিফিওমরফিক (diffeomorphic)। চিগার ও গ্রোমল অনুমান করেন যে যদি কোথাও বক্রতা কঠোরভাবে ধনাত্মক হয়, তাহলে সেই সোল একটি একক বিন্দু হতে পারে, অর্থাৎ সম্পূর্ণ স্পেস ইউক্লিডীয় স্পেসের সাথে ডিফিওমরফিক হতে পারে।
১৯৯৪ সালে, পেরেলমান চিগার ও গ্রোমলের এই অনুমান একটি সংক্ষিপ্ত প্রমাণের মাধ্যমে সমাধান করেন। তিনি দেখান যে, অ-নেতিবাচক সেকশনাল কার্ভেচারের ক্ষেত্রে শরাফুতদিনভের রিট্রাকশন একটি সাবমারশন (submersion)। এই উপপাদ্যটি দেখায়, অ-নেতিবাচক বক্রতাযুক্ত একটি মেট্রিককে এমন একটি মেট্রিকে রূপান্তর করা অসম্ভব হতে পারে যার কোথাও কঠোর ধনাত্মক বক্রতা রয়েছে।
তিনি আরও কাজ করেন বিভিন্ন রকমের ধনাত্মক রিচি কার্ভেচারযুক্ত রিম্যানীয় ম্যানিফোল্ড নির্মাণে। তিনি রিচি কার্ভেচার, সসীম ব্যাসার্ধ এবং নন-জিরো ভলিউমসহ অসংখ্য কমপ্লেক্স প্রোজেক্টিভ প্লেনের সংযুক্ত রূপে (connected sum) একটি মেট্রিক তৈরি করেন। এছাড়াও, তিনি চার-মাত্রিক ইউক্লিডীয় স্পেসে একটি পূর্ণাঙ্গ মেট্রিক তৈরি করেন যার রিচি কার্ভেচার ধনাত্মক এবং ভলিউম ইউক্লিডীয় রীতিতে বৃদ্ধি পায়।

জ্যামিতিকীকরণ ও পয়েনকারে অনুমানসমূহ
মূল প্রবন্ধ: পয়েনকারে অনুমান ও থার্স্টনের জ্যামিতিকীকরণ অনুমান
পয়েনকারে অনুমানটি, যা গণিতবিদ অঁরি পয়েনকারে ১৯০৪ সালে প্রস্তাব করেছিলেন, ২০শ শতজুড়ে টপোলজির একটি প্রধান সমস্যা হিসেবে বিবেচিত হয়েছে। ৩-স্ফিয়ার—যা চার-মাত্রিক ইউক্লিডীয় স্থানে কেন্দ্র থেকে একক দূরত্বে অবস্থিত বিন্দুগুলির সমষ্টি—এ যেকোনো লুপকে বিন্দুতে সংকুচিত করা যায়। পয়েনকারে ধারণা করেছিলেন, বিপরীতটি হয়তো সত্য: যদি কোনো বন্ধ তিন-মাত্রিক বহুবিধের এমন বৈশিষ্ট্য থাকে যে যেকোনো লুপকে বিন্দুতে সংকুচিত করা যায়, তবে তা অবশ্যই টপোলজিক্যালভাবে ৩-স্ফিয়ারের সমতুল্য হবে। স্টিফেন স্মেইল ১৯৬১ সালে পয়েনকারে অনুমানের একটি উচ্চ-মাত্রিক রূপ প্রমাণ করেন এবং মাইকেল ফ্রিডম্যান ১৯৮২ সালে চার-মাত্রিক সংস্করণটি প্রমাণ করেন। তবে তিন-মাত্রিক ক্ষেত্রে সমস্যাটি তখনো সম্পূর্ণ অমীমাংসিত ছিল। তদ্ব্যতীত, স্মেইল ও ফ্রিডম্যানের পদ্ধতিগুলোর তিন-মাত্রিক ক্ষেত্রে তেমন প্রভাব ছিল না, কারণ তাদের ব্যবহৃত টপোলজিক্যাল রূপান্তরগুলো অধিকতর মাত্রা প্রয়োজন করত।
১৯৮২ সালে উইলিয়াম থার্স্টন একটি নতুন দৃষ্টিভঙ্গি উপস্থাপন করেন, যা পয়েনকারে অনুমানকে তিন-মাত্রিক টপোলজির একটি বৃহত্তর কাঠামোবদ্ধ তত্ত্বের বিশেষ ক্ষেত্রে রূপে উপস্থাপন করে। তার প্রস্তাবিত থার্স্টন জ্যামিতিকীকরণ অনুমান অনুযায়ী, যেকোনো বন্ধ তিন-মাত্রিক বহুবিধে কিছু নির্দিষ্ট দ্বি-মাত্রিক গোলক ও টোরাস (গহ্বরযুক্ত ডোনাট-আকৃতি) থাকা উচিত, যা সেটিকে পৃথক অংশে বিভক্ত করে, এবং প্রতিটি অংশের মধ্যে একটি অভিন্ন জ্যামিতিক কাঠামো প্রয়োগ করা যায়। থার্স্টন এই অনুমানের আংশিক প্রমাণ দেন।
একই সময়ে, রিচার্ড হ্যামিল্টন "রিক্চি ফ্লো" নামক একটি তত্ত্ব উপস্থাপন করেন, যা একটি পার্শ্বীয় ডিফারেনশিয়াল সমীকরণের মাধ্যমে কোনো বহুবিধের উপর প্রয়োগ করা মেট্রিককে সময়ের সাথে বিকশিত করতে সাহায্য করে। এই পদ্ধতি, কিছু নির্দিষ্ট অবস্থায়, মেট্রিককে অভিন্ন করার ক্ষমতা রাখে।
যদিও রিক্চি ফ্লো ও তাপ সমীকরণের মধ্যে আনুষ্ঠানিক সাদৃশ্য ছিল, রিক্চি ফ্লো ছিল অনেক বেশি জটিল ও অরৈখিক। এই পদ্ধতিতে সময়ের সাথে "সিঙ্গুলারিটি" তৈরি হয়—অর্থাৎ, কিছু এলাকায় বক্রতা অসীমের দিকে ধাবিত হয়। শিং-টুং ইয়াউ ধারণা করেন যে এই সিঙ্গুলারিটির অবস্থান টপোলজিক্যালভাবে গুরুত্বপূর্ণ হতে পারে এবং থার্স্টনের অনুমানের প্রয়োজনীয় গোলক ও টোরাস নির্ধারণে সহায়ক হতে পারে। এই দৃষ্টিভঙ্গি থেকে হ্যামিল্টন বিশদ বিশ্লেষণ শুরু করেন।
১৯৯০-এর দশকে হ্যামিল্টনের কাজ রিক্চি ফ্লো ও সার্জারি (বহুবিধের কিছু অংশ বাদ দিয়ে তা ঠিক করার প্রক্রিয়া) নিয়ে গুরুত্বপূর্ণ অগ্রগতি সাধন করে। তবে তিনি তিন-মাত্রিক ক্ষেত্রে সিঙ্গুলারিটির পূর্ণ বিশ্লেষণ করতে সক্ষম হননি। ১৯৯৯ সালে তিনি দেখান যে যদি সার্জারির একটি তিন-মাত্রিক সংস্করণ তৈরি করা যায় এবং যদি দীর্ঘমেয়াদে রিক্চি ফ্লোর আচরণ সংক্রান্ত একটি অনুমান প্রমাণ করা যায়, তবে থার্স্টনের অনুমান সমাধান সম্ভব হবে। এটি "হ্যামিল্টন প্রোগ্রাম" নামে পরিচিত হয়।
পেরেলমানের কাজ
২০০২ সালের নভেম্বর ও ২০০৩ সালের মার্চ মাসে গ্রিগোরি পেরেলমান arXiv-এ দুটি প্রিপ্রিন্ট প্রকাশ করেন, যেখানে তিনি থার্স্টনের অনুমানের প্রমাণের রূপরেখা দেন। একটি তৃতীয় প্রিপ্রিন্টে তিনি পয়েনকারে অনুমান প্রমাণের জন্য একটি বিকল্প যুক্তি উপস্থাপন করেন।
তার প্রথম প্রিপ্রিন্টে দুটি প্রধান ফলাফল ছিল: প্রথমটি ছিল "নন-কলাপসিং থিওরেম", যা বলছে যে, যদি বক্রতার পরিমাণ একটি নির্দিষ্ট নিয়ন্ত্রণে থাকে, তবে সেই এলাকায় ভলিউমও নিয়ন্ত্রণযোগ্য। দ্বিতীয়টি ছিল "ক্যাননিকাল নেবারহুড থিওরেম", যা তিন-মাত্রিক রিক্চি ফ্লোর সিঙ্গুলারিটি বিশ্লেষণে একটি মাইলফলক। তিনি দেখান যে প্রতিটি সিঙ্গুলারিটি স্থানীয়ভাবে একটি সিলিন্ডার বা একটি গোলকের মতো দেখায় যা সংকুচিত হচ্ছে।
দ্বিতীয় প্রিপ্রিন্টে পেরেলমান তার পূর্ববর্তী কাজগুলো ব্যবহার করে একটি "রিক্চি ফ্লো উইথ সার্জারি" পদ্ধতি তৈরি করেন, যা তিন-মাত্রিক বহুবিধে প্রয়োগ করা যায়। এর মাধ্যমে তিনি প্রমাণ করেন যে যেসব বহুবিধে ধনাত্মক স্কেলার বক্রতা ধারণ করতে পারে, তাদের শ্রেণিবিন্যাস সম্পূর্ণভাবে নির্ধারণ করা যায়। তৃতীয় প্রিপ্রিন্টে তিনি দেখান যে যেসব ক্ষেত্র পয়েনকারে অনুমানে পড়ে, সেখানে রিক্চি ফ্লো উইথ সার্জারি একটি নির্দিষ্ট সময়ের পরেই থেমে যায়। এর ফলে পয়েনকারে অনুমান প্রমাণ হয়ে যায়।
থার্স্টনের অনুমান প্রমাণ করতে হলে রিক্চি ফ্লো উইথ সার্জারির দীর্ঘমেয়াদি বিশ্লেষণ প্রয়োজন। যদিও পেরেলমান হ্যামিল্টনের ১৯৯৯ সালের অনুমান পুরোপুরি প্রমাণ করতে পারেননি, তবুও তিনি হ্যামিল্টনের যুক্তিগুলো তার নতুন পদ্ধতির জন্য মানিয়ে নেন। তিনি এমন একটি উপপাদ্য প্রস্তাব করেন যা স্থানীয়ভাবে ভাঙনশীল বহুবিধের বৈশিষ্ট্য নির্ধারণ করে, এবং বলেন এর প্রমাণ ভবিষ্যতে প্রকাশ করবেন। যদিও তিনি তা প্রকাশ করেননি, পরবর্তীতে বিভিন্ন গবেষক (যেমন তাকাশি শিওয়া ও তাকাও ইয়ামাগুচি, জন মরগান ও গ্যাং তিয়ান প্রমুখ) তার প্রস্তাবিত তত্ত্বের প্রমাণ প্রকাশ করেন।
sourse : wikipedia
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0