অ্যান্ড্রু ওয়াইলস এর জীবনী | Biography of Andrew Wiles
অ্যান্ড্রু ওয়াইলস এর জীবনী | Biography of Andrew Wiles

অ্যান্ড্রু ওয়াইলস ব্রিটিশ গণিতবিদ
|
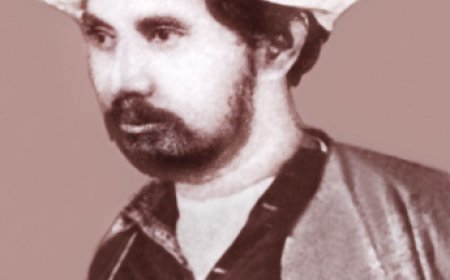
স্যার অ্যান্ড্রু ওয়াইলস
কেবিই এফআরএস
|
|
|---|---|
| জন্ম |
অ্যান্ড্রু জন ওয়াইলস
১১ এপ্রিল ১৯৫৩ (বয়স ৭২) কেমব্রিজ , ইংল্যান্ড
|
| শিক্ষা | মার্টন কলেজ, অক্সফোর্ড ( বিএ ) ক্লেয়ার কলেজ, কেমব্রিজ ( এমএ , পিএইচডি ) |
|
জন্য পরিচিত |
অর্ধস্থির উপবৃত্তাকার বক্ররেখার জন্য তানিয়ামা-শিমুরা অনুমান প্রমাণ করা , যার ফলে ফার্মাটের শেষ উপপাদ্য প্রমাণ করা ইওয়াসাওয়া তত্ত্বের মূল অনুমান প্রমাণ করা |
| পুরষ্কার |
|
|
বৈজ্ঞানিক কর্মজীবন |
|
|
ক্ষেত্র |
গণিত |
|
প্রতিষ্ঠান |
|
|
থিসিস |
পারস্পরিকতা আইন এবং বার্চ এবং সুইনারটন-ডায়ারের অনুমান (১৯৭৯) |
|
ডক্টরেট উপদেষ্টা |
জন কোটস |
| ডক্টরেট ছাত্ররা |
|
স্যার অ্যান্ড্রু জন ওয়াইলস
(জন্ম: ১১ এপ্রিল ১৯৫৩) একজন ইংরেজ গণিতবিদ এবং অক্সফোর্ড বিশ্ববিদ্যালয়ের রয়েল সোসাইটি রিসার্চ অধ্যাপক , যিনি সংখ্যা তত্ত্বের উপর বিশেষজ্ঞ। তিনি ফার্মাটের শেষ উপপাদ্য প্রমাণ করার জন্য সর্বাধিক পরিচিত , যার জন্য তিনি ২০১৬ সালের অ্যাবেল পুরস্কার এবং ২০১৭ সালের কোপলি পদক লাভ করেন এবং যার জন্য তিনি ২০০০ সালে নাইট কমান্ডার অফ দ্য অর্ডার অফ দ্য ব্রিটিশ এম্পায়ার নিযুক্ত হন। ২০১৮ সালে, ওয়াইলস অক্সফোর্ডে গণিতের প্রথম রেজিয়াস অধ্যাপক নিযুক্ত হন। ওয়াইলস ১৯৯৭ সালের ম্যাকআর্থার ফেলোও ।
ওয়াইলসের জন্ম কেমব্রিজে ধর্মতত্ত্ববিদ মরিস ফ্রাঙ্ক ওয়াইলস এবং প্যাট্রিসিয়া ওয়াইলসের ঘরে। নাইজেরিয়ায় শৈশবের বেশিরভাগ সময় কাটানোর সময়, ওয়াইলস গণিত এবং বিশেষ করে ফার্মাটের শেষ উপপাদ্যের প্রতি আগ্রহ তৈরি করেন। ১৯৭৪ সালে অক্সফোর্ডে চলে আসার পর এবং সেখান থেকে স্নাতক হওয়ার পর, তিনি গ্যালোয়া উপস্থাপনা , উপবৃত্তাকার বক্ররেখা এবং মডুলার ফর্মগুলিকে একীভূত করার জন্য কাজ করেন, যার শুরু ব্যারি মাজুরের ইওয়াসাওয়া তত্ত্বের সাধারণীকরণ থেকে । ১৯৮০-এর দশকের গোড়ার দিকে, ওয়াইলস প্রিন্সটন বিশ্ববিদ্যালয়ে যাওয়ার আগে কয়েক বছর কেমব্রিজ বিশ্ববিদ্যালয়ে কাটিয়েছিলেন, যেখানে তিনি হিলবার্ট মডুলার ফর্মগুলি সম্প্রসারণ এবং প্রয়োগের উপর কাজ করেছিলেন । ১৯৮৬ সালে, ফার্মাটের শেষ উপপাদ্যের উপর কেন রিবেটের মৌলিক কাজ পড়ার পর, ওয়াইলস সেমিস্টেবল উপবৃত্তাকার বক্ররেখার জন্য মডুলারিটি উপপাদ্য প্রমাণ করার জন্য যাত্রা শুরু করেন , যা ফার্মাটের শেষ উপপাদ্যকে বোঝায়। ১৯৯৩ সালের মধ্যে, তিনি একজন জ্ঞানী সহকর্মীকে বোঝাতে সক্ষম হন যে তার কাছে ফার্মাটের শেষ উপপাদ্যের প্রমাণ রয়েছে, যদিও পরবর্তীতে একটি ত্রুটি আবিষ্কৃত হয়। ১৯৯৪ সালের ১৯ সেপ্টেম্বর একটি অন্তর্দৃষ্টির পর, ওয়াইলস এবং তার ছাত্র রিচার্ড টেলর ত্রুটিটি এড়াতে সক্ষম হন এবং ১৯৯৫ সালে ফলাফল প্রকাশ করেন, যা ব্যাপক প্রশংসা অর্জন করে।
ফার্মাটের শেষ উপপাদ্য প্রমাণ করার সময়, ওয়াইলস গণিতবিদদের জন্য ভিন্ন ধারণা এবং উপপাদ্যগুলিকে একত্রিত করার জন্য নতুন সরঞ্জাম তৈরি করেছিলেন। তার প্রাক্তন ছাত্র টেলর এবং আরও তিনজন গণিতবিদ ওয়াইলসের কাজ ব্যবহার করে 2000 সালের মধ্যে সম্পূর্ণ মডুলারিটি উপপাদ্য প্রমাণ করতে সক্ষম হন। 2016 সালে অ্যাবেল পুরষ্কার পাওয়ার পর, ওয়াইলস তার উত্তরাধিকারের উপর প্রতিফলন করেন, তার বিশ্বাস প্রকাশ করেন যে তিনি কেবল ফার্মাটের শেষ উপপাদ্য প্রমাণ করেননি, বরং সমগ্র গণিতকে ল্যাংল্যান্ডস সংখ্যা তত্ত্বকে একত্রিত করার প্রোগ্রামের দিকে ঠেলে দিয়েছেন।
শিক্ষা এবং প্রাথমিক জীবন
ওয়াইলসের জন্ম ১৯৫৩ সালের ১১ এপ্রিল ইংল্যান্ডের কেমব্রিজে , তিনি মরিস ফ্রাঙ্ক ওয়াইলস (১৯২৩-২০০৫) এবং প্যাট্রিসিয়া ওয়াইলস (née Mowll) এর পুত্র। ১৯৫২ থেকে ১৯৫৫ সাল পর্যন্ত, তার বাবা কেমব্রিজের রিডলি হলে চ্যাপেলিন হিসেবে কাজ করেছিলেন এবং পরে অক্সফোর্ড বিশ্ববিদ্যালয়ের ডিভিনিটির রেজিয়াস অধ্যাপক হন ।
ওয়াইলস নাইজেরিয়ায় তার আনুষ্ঠানিক শিক্ষাজীবন শুরু করেছিলেন, যখন তিনি খুব ছোটবেলায় তার বাবা-মায়ের সাথে সেখানে থাকতেন। তবে, তার বাবা-মায়ের লেখা চিঠি অনুসারে, ক্লাসে যোগদানের কথা থাকার পর অন্তত প্রথম কয়েক মাস তিনি যেতে অস্বীকৃতি জানান। এই তথ্য থেকে, ওয়াইলস নিজেই এই সিদ্ধান্তে উপনীত হন যে তার প্রথম বছরগুলিতে, তিনি শিক্ষা প্রতিষ্ঠানে সময় কাটাতে উৎসাহী ছিলেন না। ২০২১ সালে নাদিয়া হাসনাউইয়ির সাথে এক সাক্ষাৎকারে , তিনি বলেছিলেন যে তিনি চিঠিপত্রগুলিতে বিশ্বাস করতেন, তবুও তিনি এমন একটি সময় মনে করতে পারেননি যখন তিনি গাণিতিক সমস্যা সমাধান করতে পছন্দ করতেন না।
ওয়াইলস কেমব্রিজের কিংস কলেজ স্কুলে এবং কেমব্রিজের দ্য লেইস স্কুলে পড়াশোনা করেছেন । ওয়াইলস ১৯৯৯ সালে WGBH-TV কে বলেন যে ১০ বছর বয়সে স্কুল থেকে বাড়ি ফেরার পথে তিনি ফার্মাটের শেষ উপপাদ্যটি দেখতে পান। তিনি তার স্থানীয় লাইব্রেরিতে থামেন যেখানে তিনি এরিক টেম্পল বেলের লেখা " দ্য লাস্ট প্রবলেম" বইটি খুঁজে পান , যা উপপাদ্য সম্পর্কে। একটি উপপাদ্যের অস্তিত্ব দেখে মুগ্ধ হয়েছিলেন যা বলা এত সহজ ছিল যে তিনি, দশ বছর বয়সী, এটি বুঝতে পারতেন, কিন্তু কেউ প্রমাণ করতে পারেননি, তিনি এটি প্রমাণ করার জন্য প্রথম ব্যক্তি হওয়ার সিদ্ধান্ত নিয়েছিলেন। যাইহোক, তিনি শীঘ্রই বুঝতে পেরেছিলেন যে তার জ্ঞান খুব সীমিত, তাই তিনি তার শৈশবের স্বপ্ন পরিত্যাগ করেছিলেন যতক্ষণ না কেন রিবেটের ১৯৮৬ সালে অ্যাপসিলন অনুমানের প্রমাণ দ্বারা এটি তার নজরে আসে , যা গেরহার্ড ফ্রে পূর্বে ফার্মাটের সমীকরণের সাথে যুক্ত করেছিলেন।
প্রাথমিক কর্মজীবন
১৯৭৪ সালে, ওয়াইলস অক্সফোর্ডের মার্টন কলেজ থেকে গণিতে স্নাতক ডিগ্রি অর্জন করেন । ওয়াইলসের স্নাতক গবেষণা ১৯৭৫ সালের গ্রীষ্মে জন কোটসের নেতৃত্বে শুরু হয়েছিল। তারা একসাথে ইওয়াসাওয়া তত্ত্বের পদ্ধতি দ্বারা জটিল গুণনের সাথে উপবৃত্তাকার বক্ররেখার পাটিগণিত নিয়ে কাজ করেছিলেন । তিনি ব্যারি মাজুরের সাথে যুক্তিসঙ্গত সংখ্যার উপর ইওয়াসাওয়া তত্ত্বের মূল অনুমান নিয়ে আরও কাজ করেছিলেন এবং এর পরেই, তিনি এই ফলাফলকে সম্পূর্ণ বাস্তব ক্ষেত্রে সাধারণীকরণ করেছিলেন ।
১৯৮০ সালে, ওয়াইলস কেমব্রিজের ক্লেয়ার কলেজে পিএইচডি ডিগ্রি অর্জন করেন । ১৯৮১ সালে নিউ জার্সির প্রিন্সটনে ইনস্টিটিউট ফর অ্যাডভান্সড স্টাডিতে থাকার পর , ওয়াইলস প্রিন্সটন বিশ্ববিদ্যালয়ে গণিতের অধ্যাপক হন ।
1985-86 সালে, ওয়াইলস প্যারিসের কাছে ইনস্টিটিউট দেস হাউটেস ইটুডেস সায়েন্টিফিকেস এবং ইকোলে নরমাল সুপারিউরে একজন গুগেনহেইম ফেলো ছিলেন ।
১৯৮৯ সালে, ওয়াইলস রয়েল সোসাইটিতে নির্বাচিত হন । তার নির্বাচনী শংসাপত্র অনুসারে, তিনি " হিলবার্ট মডুলার ফর্মের সাথে সংযুক্ত ℓ-অ্যাডিক উপস্থাপনা নির্মাণের উপর কাজ করছিলেন এবং সম্পূর্ণ বাস্তব ক্ষেত্রের সাইক্লোটমিক এক্সটেনশনের জন্য 'প্রধান অনুমান' প্রমাণ করার জন্য এগুলি প্রয়োগ করেছিলেন"।
ফার্মাটের শেষ উপপাদ্যের প্রমাণ
১৯৮৮ থেকে ১৯৯০ সাল পর্যন্ত, ওয়াইলস অক্সফোর্ড বিশ্ববিদ্যালয়ে রয়েল সোসাইটি রিসার্চ অধ্যাপক ছিলেন এবং তারপর তিনি প্রিন্সটনে ফিরে আসেন। ১৯৯৪ থেকে ২০০৯ সাল পর্যন্ত, ওয়াইলস প্রিন্সটনে ইউজিন হিগিন্স অধ্যাপক ছিলেন।
১৯৮৬ সালের মাঝামাঝি থেকে, গেরহার্ড ফ্রে , জিন-পিয়ের সেরে এবং কেন রিবেটের পূর্ববর্তী কয়েক বছরের ধারাবাহিক অগ্রগতির উপর ভিত্তি করে , এটি স্পষ্ট হয়ে ওঠে যে ফার্মাটের শেষ উপপাদ্য (এই বিবৃতি যে কোনও তিনটি ধনাত্মক পূর্ণসংখ্যা a , b , এবং c সমীকরণ a n + b n = c n এর সাথে 2 এর বেশি n এর পূর্ণসংখ্যার মান পূরণ করে না ) মডুলারিটি উপপাদ্যের একটি সীমিত রূপের ফলাফল হিসাবে প্রমাণিত হতে পারে (সেই সময়ে অপ্রমাণিত এবং তখন "তানিয়ামা-শিমুরা-ওয়েইল অনুমান" নামে পরিচিত)। মডুলারিটি উপপাদ্যটি উপবৃত্তাকার বক্ররেখা জড়িত ছিল, যা ওয়াইলসের নিজস্ব বিশেষজ্ঞ ক্ষেত্রও ছিল এবং বলেছিল যে এই জাতীয় সমস্ত বক্ররেখার সাথে একটি মডুলার রূপ যুক্ত রয়েছে। এই বক্ররেখাগুলিকে টরাসের পৃষ্ঠের সমাধানের অনুরূপ গাণিতিক বস্তু হিসাবে ভাবা যেতে পারে, এবং যদি ফার্মাটের শেষ উপপাদ্যটি মিথ্যা হয় এবং সমাধান বিদ্যমান থাকে, তাহলে "একটি অদ্ভুত বক্ররেখা তৈরি হবে"। অতএব, উপপাদ্যের প্রমাণ হিসেবে দেখানো হবে যে এই ধরণের বক্ররেখার অস্তিত্ব থাকবে না।
সমসাময়িক গণিতবিদরা এই অনুমানকে গুরুত্বপূর্ণ হিসেবে দেখেছিলেন, কিন্তু প্রমাণ করা অসাধারণভাবে কঠিন বা সম্ভবত অসম্ভব। উদাহরণস্বরূপ, ওয়াইলসের প্রাক্তন তত্ত্বাবধায়ক জন কোটস বলেছিলেন যে এটি "প্রকৃতপক্ষে প্রমাণ করা অসম্ভব" বলে মনে হয়েছিল, : 226 এবং কেন রিবেট নিজেকে "[এটি] সম্পূর্ণরূপে অ্যাক্সেসযোগ্য বলে বিশ্বাসকারী বিশাল সংখ্যাগরিষ্ঠ লোকের একজন" বলে মনে করেছিলেন, আরও যোগ করেছেন যে "অ্যান্ড্রু ওয়াইলস সম্ভবত পৃথিবীর সেই কয়েকজন মানুষের মধ্যে একজন ছিলেন যাদের স্বপ্ন দেখার সাহস ছিল যে আপনি আসলে গিয়ে [এটি] প্রমাণ করতে পারবেন।
তা সত্ত্বেও, ওয়াইলস, ফার্ম্যাটের শেষ উপপাদ্যের প্রতি তার শৈশবকাল থেকেই আকর্ষণের কারণে, অনুমান প্রমাণের চ্যালেঞ্জ গ্রহণ করার সিদ্ধান্ত নেন, অন্তত ফ্রেয়ের বক্ররেখার জন্য প্রয়োজনীয় পরিমাণে তিনি প্রায় সম্পূর্ণ গোপনীয়তার মধ্যে ছয় বছরেরও বেশি সময় ধরে এই সমস্যাটির জন্য তার সমস্ত গবেষণা সময় উৎসর্গ করেছিলেন, পূর্বের কাজগুলি ছোট ছোট অংশে পৃথক কাগজপত্র হিসাবে প্রকাশ করে এবং কেবল তার স্ত্রীর উপর গোপন রেখে তার প্রচেষ্টাকে আড়াল করেছিলেন।
ওয়াইলসের গবেষণায় ফার্মাটের শেষ উপপাদ্যের বিপরীতে একটি প্রমাণ তৈরি করা জড়িত ছিল, যা রিবেট তার ১৯৮৬ সালের গবেষণায় খুঁজে পেয়েছিলেন যে একটি উপবৃত্তাকার বক্ররেখা আছে এবং তাই সত্য হলে একটি সংশ্লিষ্ট মডুলার রূপ রয়েছে। উপপাদ্যটি ভুল বলে ধরে নিয়ে শুরু করে, ওয়াইলস তারপর সেই অনুমানের অধীনে প্রণীত তানিয়ামা-শিমুরা-ওয়েইল অনুমানের বিপরীতে রিবেটের উপপাদ্যের সাথে (যা বলেছিল যে যদি n একটি মৌলিক সংখ্যা হয় , তাহলে এই ধরণের কোনও উপবৃত্তাকার বক্ররেখার একটি মডুলার রূপ থাকতে পারে না, তাই ফার্মাটের সমীকরণের কোনও অদ্ভুত মৌলিক প্রতি-উদাহরণ থাকতে পারে না)। ওয়াইলস আরও প্রমাণ করেছিলেন যে অনুমানটি সেমিস্টেবল উপবৃত্তাকার বক্ররেখা নামে পরিচিত বিশেষ ক্ষেত্রে প্রযোজ্য যার সাথে ফার্মাটের সমীকরণটি আবদ্ধ ছিল। অন্য কথায়, ওয়াইলস আবিষ্কার করেছিলেন যে ফার্মাটের সমীকরণের ক্ষেত্রে তানিয়ামা-শিমুরা-ওয়েইল অনুমান সত্য ছিল, এবং রিবেটের আবিষ্কার (যে অর্ধস্থির উপবৃত্তাকার বক্ররেখার জন্য অনুমান ধারণের অর্থ ফার্মাটের শেষ উপপাদ্য সত্য হতে পারে) জয়লাভ করেছিল, এইভাবে ফার্মাটের শেষ উপপাদ্য প্রমাণিত হয়েছিল।
১৯৯৩ সালের জুন মাসে, তিনি কেমব্রিজে একটি সম্মেলনে প্রথমবারের মতো জনসাধারণের সামনে তার প্রমাণ উপস্থাপন করেন। দ্য নিউ ইয়র্ক টাইমসের জিনা কোলাটা উপস্থাপনার সারসংক্ষেপ নিম্নরূপে তুলে ধরেন:
তিনি সোমবার, মঙ্গলবার এবং বুধবার প্রতিদিন "মডুলার ফর্ম, উপবৃত্তাকার বক্ররেখা এবং গ্যালোয়া প্রতিনিধিত্ব" শিরোনামে একটি বক্তৃতা দিয়েছিলেন। ডঃ রিবেট বলেন, শিরোনামে এমন কোনও ইঙ্গিত ছিল না যে ফার্মাটের শেষ উপপাদ্য নিয়ে আলোচনা করা হবে। ... অবশেষে, তার তৃতীয় বক্তৃতার শেষে, ডঃ ওয়াইলস উপসংহারে পৌঁছেছিলেন যে তিনি তানিয়ামা অনুমানের একটি সাধারণ ঘটনা প্রমাণ করেছেন। তারপর, আপাতদৃষ্টিতে একটি পরবর্তী চিন্তাভাবনা হিসাবে, তিনি উল্লেখ করেছিলেন যে এর অর্থ হল ফার্মাটের শেষ উপপাদ্য সত্য। QED
১৯৯৩ সালের আগস্টে, এটি আবিষ্কৃত হয় যে প্রমাণটিতে সেলমার গ্রুপের বৈশিষ্ট্য এবং অয়লার সিস্টেম নামক একটি হাতিয়ারের ব্যবহারের সাথে সম্পর্কিত বেশ কয়েকটি ক্ষেত্রে ত্রুটি রয়েছে । ওয়াইলস এক বছরেরও বেশি সময় ধরে তার প্রমাণ মেরামত করার চেষ্টা করেছিলেন এবং ব্যর্থ হন। ওয়াইলসের মতে, এই অঞ্চলটি বন্ধ করার পরিবর্তে - circumventing এর জন্য গুরুত্বপূর্ণ ধারণাটি তার কাছে আসে ১৯ সেপ্টেম্বর ১৯৯৪ সালে, যখন তিনি হাল ছেড়ে দেওয়ার পথে ছিলেন। circumvention উপবৃত্তাকার বক্ররেখা প্রতিস্থাপনের জন্য গ্যালোয়া উপস্থাপনা ব্যবহার করে , সমস্যাটিকে একটি শ্রেণী সংখ্যা সূত্রে হ্রাস করে এবং অন্যান্য বিষয়গুলির মধ্যে এটি সমাধান করে, সমস্ত কিছু ভিক্টর কোলিভ্যাগিনের ধারণাগুলিকে ইওয়াসাওয়া তত্ত্বের সাথে ম্যাথিয়াস ফ্ল্যাচের পদ্ধতি ঠিক করার ভিত্তি হিসাবে ব্যবহার করে। তার প্রাক্তন ছাত্র রিচার্ড টেলরের সাথে , ওয়াইলস একটি দ্বিতীয় গবেষণাপত্র প্রকাশ করেন যাতে circumvention অন্তর্ভুক্ত ছিল এবং এইভাবে প্রমাণটি সম্পূর্ণ করে। উভয় গবেষণাপত্রই ১৯৯৫ সালের মে মাসে অ্যানালস অফ ম্যাথমেটিক্সের একটি নিবেদিত সংখ্যায় প্রকাশিত হয়েছিল ।
পরবর্তী কর্মজীবন
২০১১ সালে, ওয়াইলস অক্সফোর্ড বিশ্ববিদ্যালয়ে রয়েল সোসাইটি রিসার্চ প্রফেসর হিসেবে পুনরায় যোগদান করেন।
২০১৮ সালের মে মাসে, ওয়াইলসকে অক্সফোর্ডে গণিতের রেগিয়াস অধ্যাপক নিযুক্ত করা হয় , যা বিশ্ববিদ্যালয়ের ইতিহাসে প্রথম।
উত্তরাধিকার
গণিতের অনেক ক্ষেত্রে ওয়াইলসের কাজ ব্যবহার করা হয়েছে। উল্লেখযোগ্যভাবে, ১৯৯৯ সালে, তার তিন প্রাক্তন ছাত্র, রিচার্ড টেলর , ব্রায়ান কনরাড এবং ফ্রেড ডায়মন্ড , ক্রিস্টোফ ব্রুইলের সাথে কাজ করে , সম্পূর্ণ মডুলারিটি উপপাদ্য প্রমাণ করার জন্য ওয়াইলসের প্রমাণের উপর ভিত্তি করে তৈরি করেছিলেন। ওয়াইলসের ডক্টরেট ছাত্রদের মধ্যে মঞ্জুল ভার্গব (২০১৪ সালে ফিল্ডস মেডেল বিজয়ী ), এহুদ ডি শালিত , ঋতব্রত মুন্সি ( এসএসবি পুরস্কার এবং আইসিটিপি রামানুজন পুরস্কার বিজয়ী ), কার্ল রুবিন ( ভেরা রুবিনের পুত্র ), ক্রিস্টোফার স্কিনার এবং বিনায়ক ভাতসাল (২০০৭ সালে কক্সেটার-জেমস পুরস্কার বিজয়ী ) অন্তর্ভুক্ত ছিলেন।
২০১৬ সালে, অ্যাবেল পুরষ্কার পাওয়ার পর , ওয়াইলস ফার্মাটের শেষ উপপাদ্যের প্রমাণ সম্পর্কে বলেছিলেন, "যে পদ্ধতিগুলি এটি সমাধান করেছিল তা সমসাময়িক গণিতের অনুমানের একটি বৃহৎ জালকে আক্রমণ করার একটি নতুন উপায় খুলে দিয়েছে, যা ল্যাংল্যান্ডস প্রোগ্রাম নামে পরিচিত , যা একটি মহান দৃষ্টিভঙ্গি হিসাবে গণিতের বিভিন্ন শাখাকে একত্রিত করার চেষ্টা করে। এটি আমাদের এটি দেখার একটি নতুন উপায় দিয়েছে"।
পুরষ্কার এবং সম্মানন

ফার্মাটের শেষ উপপাদ্য সম্পর্কে ওয়াইলসের প্রমাণ বিশ্বের অন্যান্য গাণিতিক বিশেষজ্ঞদের তদন্তের সামনে দাঁড়িয়েছে। ফার্মাটের শেষ উপপাদ্য সম্পর্কে বিবিসির তথ্যচিত্র সিরিজ হরাইজন এর একটি পর্বের জন্য ওয়াইলসের সাক্ষাৎকার নেওয়া হয়েছিল। এটি পিবিএস বিজ্ঞান টেলিভিশন সিরিজ নোভার একটি পর্ব হিসাবে "দ্য প্রুফ" শিরোনামে সম্প্রচারিত হয়েছিল। সাইমন সিং -এর জনপ্রিয় বই ফার্মাটের শেষ উপপাদ্য- তেও তার কাজ এবং জীবন বিশদভাবে বর্ণনা করা হয়েছে ।
১৯৮৮ সালে, ওয়াইলস লন্ডন ম্যাথমেটিক্যাল সোসাইটির জুনিয়র হোয়াইটহেড পুরস্কার (১৯৮৮) লাভ করেন । ১৯৮৯ সালে, তিনি রয়েল সোসাইটির (FRS) ফেলো নির্বাচিত হন
১৯৯৪ সালে, ওয়াইলস আমেরিকান একাডেমি অফ আর্টস অ্যান্ড সায়েন্সেসের সদস্য নির্বাচিত হন । ১৯৯৫ সালে ফার্মাটের শেষ উপপাদ্যের প্রমাণ সম্পন্ন করার পর, তিনি সেই বছর শক পুরস্কার , ফার্মাট পুরস্কার , এবং গণিতে উলফ পুরস্কার লাভ করেন। ওয়াইলস ন্যাশনাল একাডেমি অফ সায়েন্সেসের একজন বিদেশী সহযোগী নির্বাচিত হন এবং ন্যাশনাল একাডেমি অফ সায়েন্সেস থেকে গণিতে NAS পুরস্কার , রয়েল মেডেল এবং ১৯৯৬ সালে অস্ট্রোস্কি পুরস্কার লাভ করেন। তিনি আমেরিকান ম্যাথমেটিক্যাল সোসাইটির কোল পুরস্কার , ম্যাকআর্থার ফেলোশিপ এবং ১৯৯৭ সালে উলফস্কেল পুরস্কার লাভ করেন, এবং সেই বছর আমেরিকান ফিলোসফিক্যাল সোসাইটির সদস্য নির্বাচিত হন ।
১৯৯৮ সালে, ওয়াইলসকে আন্তর্জাতিক গণিত ইউনিয়ন থেকে তার কৃতিত্বের স্বীকৃতিস্বরূপ একটি রৌপ্য ফলক প্রদান করা হয়, ফিল্ডস মেডেলের পরিবর্তে , যা ৪০ বছরের কম বয়সীদের জন্য সীমাবদ্ধ (১৯৯৪ সালে যখন ওয়াইলস উপপাদ্যটি প্রমাণ করেছিলেন তখন তার বয়স ছিল ৪১)। একই বছর, তাকে ১৯৯৯ সালে ক্লে রিসার্চ অ্যাওয়ার্ডের সাথে বাদশাহ ফয়সাল পুরস্কার , প্রদান করা হয়, যে বছর গ্রহাণুটি 9999 ওয়াইলসের নামকরণ করা হয়েছিল তার নামে।
২০০০ সালে, তিনি নাইট কমান্ডার অফ দ্য অর্ডার অফ দ্য ব্রিটিশ এম্পায়ার (২০০০) পুরষ্কার পান ২০০৪ সালে ওয়াইলস প্রিমিও পিটাগোরা জিতেছিলেন। ২০০৫ সালে, তিনি শ পুরস্কার জিতেছিলেন ।
অক্সফোর্ড বিশ্ববিদ্যালয়ের ম্যাথমেটিক্যাল ইনস্টিটিউটের ভবনটি ২০১৬ সালে ওয়াইলসের নামে নামকরণ করা হয়। পরে সেই বছর তিনি অ্যাবেল পুরস্কার জিতেছিলেন । ২০১৭ সালে, ওয়াইলস কোপলি পদক জিতেছিলেন ২০১৯ সালে, তিনি ডি মরগান পদক জিতেছিলেন ।
তাঁর প্রবন্ধ “Modular Elliptic Curves and Fermat’s Last Theorem” প্রকাশিত হয় Annals of Mathematics-এর ১৪১তম খণ্ডের ৩য় সংখ্যায় (১৯৯৫), পৃষ্ঠা ৪৪৩–৫৫১। এর সঙ্গে একটি অতিরিক্ত প্রবন্ধও প্রকাশিত হয়, শিরোনাম “Ring-Theoretic Properties of Certain Hecke Algebras”, যা তিনি রিচার্ড টেইলরের সঙ্গে সহলেখক হিসেবে রচনা করেন। ২০০০ সালে ওয়াইলস নাইট উপাধিতে ভূষিত হন।
sourse:wikipedia
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0