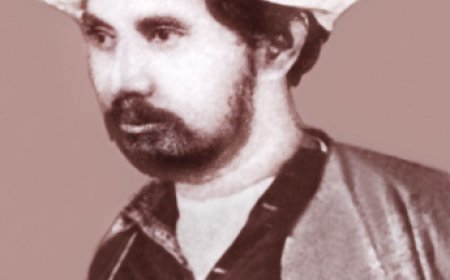
কার্ল ফ্রিডরিখ গাউস এর জীবনী | Biography of Carl Friedrich Gauss
কার্ল ফ্রিডরিখ গাউস এর জীবনী | Biography of Carl Friedrich Gauss

কার্ল ফ্রেডরিক গাউস: গণিতের রাজপুত্র
|
জন্ম |
৩০ এপ্রিল ১৭৭৭ ব্রাউনশ্ভাইগ, ব্রুন্সভিক-লুনেবুর্গের নির্বাচনী এলাকা, পবিত্র রোমান সাম্রাজ্য
|
|---|---|
|
মৃত্যু |
২৩ ফেব্রুয়ারি ১৮৫৫ (বয়স ৭৭) গোটিঙেন, হানোভার
|
|
জাতীয়তা |
জার্মানি |
|
মাতৃশিক্ষায়তন |
হেল্মষ্টেট বিশ্ববিদ্যালয় |
|
পরিচিতির কারণ |
সংখ্যা তত্ত্ব গাউসীয় চুম্বকত্ব |
|
পুরস্কার |
কপলি পদক (১৮৩৮) |
|
বৈজ্ঞানিক কর্মজীবন |
|
|
কর্মক্ষেত্র |
গণিত ও পদার্থবিজ্ঞান |
|
প্রতিষ্ঠানসমূহ |
গেয়র্গ-আউগুস্ট বিশ্ববিদ্যালয় |
|
ডক্টরাল উপদেষ্টা |
ইয়োহান ফ্রিডরিশ ফাফ |
|
অন্যান্য উচ্চশিক্ষায়তনিক উপদেষ্টা |
ইয়োহান ক্রিস্টিয়ান মার্টিন বার্টেলস |
| ডক্টরেট শিক্ষার্থী | ফ্রিড্রিশ বেসেল ক্রিস্টফ গূডারমান ক্রিস্টিয়ান লুডভিগ গের্লিং রিচার্ড ডেডেকিন্ড ইয়োহান ফ্রান্ত্স এঙ্কে ইয়োহান বেনেডিক্ট লিস্টিং বের্নহার্ট রিমান ক্রিস্টিয়ান হাইনরিখ ফ্রিডরিখ পেটার্স মরিৎস কান্টর |
|
অন্যান্য উল্লেখযোগ্য শিক্ষার্থী |
আউগুস্ট ফের্ডিনান্ড মোবিউস ইউলিয়ুস ভাইসবাখ এল. সি. শ্নুরলাইন |
|
যাদেরকে প্রভাবিত করেছেন |
সোফি জের্মাঁ |
ইয়োহান কার্ল ফ্রিডরিশ গাউস
(ⓘ: ইয়োহান্ কাল্ ফ্রিড্রিশ্ গাউস্; জার্মান ভাষায়: Johann Carl Friedrich Gauß) (৩০শে এপ্রিল, ১৭৭৭ - ২৩শে ফেব্রুয়ারি, ১৮৫৫) একজন প্রতিভাবান জার্মান গণিতবিদ এবং বিজ্ঞানী। গণিত ও বিজ্ঞানের প্রায় সকল বিভাগে তার অবদান আছে। তাকে "গণিতের যুবরাজ" ও "সর্বকালের সেরা গণিতবিদ" বলা হয়। গণিতের যে সব বিষয়ে তার অবদান আছে সেগুলোর মধ্যে আছে সংখ্যা তত্ত্ব, গাণিতিক বিশ্লেষণ, অন্তরক জ্যামিতি, চুম্বকের ধর্ম, আলোকবিজ্ঞান, জ্যোতির্বিজ্ঞান ইত্যাদি। গণিত এবং বিজ্ঞানের বহু শাখায় তার প্রশংসাযোগ্য প্রভাব ছিল, যে কারণে তাকে ইতিহাসের অন্যতম প্রভাবশালী গণিতবিদদের একজন হিসেবে বিবেচনা করা হয়।
গাউস ছোটবেলা থেকেই অসম্ভব প্রতিভাবান ছিলেন । ছোটবেলার তার গাণিতিক প্রতিভা নিয়ে অনেক গল্প শোনা যায়। তিনি কৈশোরেই তার প্রথম গুরুত্বপূর্ণ গাণিতিক আবিষ্কারগুলো সম্পাদন করেন। ১৭৯৮ সালে মাত্র ২১ বছর বয়সে তিনি তার জীবনের সর্বশ্রেষ্ঠ কাজ ডিসকিশিয়নেস অ্যারিথমেটিকা লেখা সমাপ্ত করেন, যা ১৮০১ সালে প্রকাশিত হয়। তার এই কাজ গণিতের একটি পৃথক শাখা হিসেবে সংখ্যাতত্ত্বের ভিত্তি স্থাপন করে এবং আজও এর প্রভাব অপরিসীম।
শৈশব ও কৈশোর (১৭৭৭–১৭৯৮)
কার্ল ফ্রিডরিশ গাউস ১৭৭৭ সালের ৩০ এপ্রিল জন্মগ্রহণ করেন বর্তমান নিম্ন জাখসেন অঞ্চলের অন্তর্গত ব্রাউনশ্ভাইগ শহরে। তার পিতামাতা ছিলেন নিতান্তই খেটে-খাওয়া শ্রেণীর। শৈশবেই তিনি তার গাণিতিক প্রতিভার পরিচয় দিতে শুরু করেন। তার অসাধারণ প্রতিভা সম্বন্ধে বেশ কিছু গল্প প্রচলিত আছে। কথিত আছে মাত্র তিন বছর বয়সে তিনি তার বাবার হিসাবের খাতার ভুল ধরে দেন মনে মনে গণনা করে। তার সম্বন্ধে আরেকটি বহুল প্রচলিত গল্প হচ্ছে- একবার তার প্রাথমিক বিদ্যালয়ের শিক্ষক দুষ্টু ছাত্রদের ব্যস্ত রাখবার জন্যে ১ থেকে ১০০ পর্যন্ত সংখ্যাগুলো যোগ করতে বলেন। গাউস তার শিক্ষককে অবাক করে দিয়ে মুহুর্তের মধ্যেই সঠিক উত্তরটি বের করে ফেলেন।
গাউসের যোগ করার পদ্ধতিটি ছিল অত্যন্ত সহজ - তিনি লক্ষ্য করেন ধারাটির দুই বিপরীত দিক থেকে পদ নিয়ে জোড়া তৈরি করতে থাকলে তাদের যোগফল সমান থাকে 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, এবং এভাবে সম্পূর্ণ যোগফলটি দাঁড়ায় 50 × 101 = 5050। তবে এই গল্পটির বিস্তারিত বিবরণ কিছুটা অনুমান করা বলেই মনে করা হয়; কিছু লেখক, যেমন জোসেফ রটম্যান তার বই এ ফার্স্ট কোর্স ইন এলজেবরাতে ঘটনাটি আদৌ ঘটেছিল কিনা তা নিয়েই সন্দেহ প্রকাশ করেছেন।
গাউসের বুদ্ধিবৃত্তিক ক্ষমতা ব্রাউনশ্ভাইগের ডিউকের নজর কাড়ে, যিনি তাকে কলোজিয়াম কারোলিনামে (বর্তমান টেকনিশে উইনিভার্সিটেট ব্রাউনশ্ভাইগ)-এ পড়ালেখা করবার সুযোগ করে দেন। তিনি ১৭৯২ থেকে ১৭৯৫ পর্যন্ত সেখানে অধ্যয়ন করেন এবং তারপর গোটিঙেন গেয়র্গ-আউগুস্ট বিশ্ববিদ্যালয়ে ১৭৯৫ থেকে ১৭৯৮ পর্যন্ত পড়েন।
বিশ্ববিদ্যালয়ে অধ্যয়নরত অবস্থায় গাউস বেশ কিছু গুরুত্বপূর্ণ উপপাদ্য নতুন করে আবিষ্কার করেন এবং ১৭৯৬ সালে তিনি প্রথমবারের মতো গুরুত্বপূর্ণ সাফল্য অর্জন করেন; তিনি প্রমাণ করতে সক্ষম হন যে যেসব সুষম বহুভুজের সংখ্যা ফের্মা মৌলিক সংখ্যা (এবং, সেই সাথে যেসব বহুভুজের বাহুর সংখ্যা ভিন্ন ভিন্ন ফের্মা মৌলিক সংখ্যা ও ২ এর ঘাতের গুণফল) তাদের কম্পাস ও দাগ-না-কাটা রুলার ব্যবহার করে আঁকা সম্ভব। এ আবিষ্কারটি গণিতের ক্ষেত্রে একটি অত্যন্ত গুরুত্বপূর্ণ আবিষ্কার ছিল; অঙ্কণের সমস্যা গণিতবিদদের প্রাচীন গ্রিক আমল থেকেই ভাবিয়ে আসছিল, এবং এই আবিষ্কারই গাউসকে ভাষাবিজ্ঞানের পরিবর্তে গণিতকে পেশা হিসেবে বেছে নিতে অনুপ্রাণিত করে।
গাউস তার এই উদ্ভাবন নিয়ে অত্যন্ত গর্ববোধ করতেন এবং তার ইচ্ছে ছিল তার স্মৃতিফলকে একটি সুষম সপ্তদশভুজ (heptadecagon) খোদাই করা থাকবে। তবে কারিগররা এতে অপারগতা প্রকাশ করে, কারণ সপ্তদশভুজ খোদাই করা বেশ কঠিন ব্যাপার ছিল, এবং এই শ্রমসাধ্য সপ্তদশভুজকে ভালোভাবে লক্ষ্য না করলে বৃত্তের সাথে পার্থক্য করা যেত না।
১৭৯৬ সালটি ছিল গাউস এবং সংখ্যাতত্ত্ব উভয়ের জন্যেই অন্যতম সফল একটি বছর। মার্চের ৩০ তারিখ তিনি সপ্তদশভুজ অঙ্কনের একটি কৌশল উদ্ভাবন করেন। তিনি মডিউলভিত্তিক পাটীগণিত আবিষ্কার করেন, যা সংখ্যাতাত্ত্বিক হিসাব-নিকাশ বহুগুণ সহজতর করে। তিনি 8 এপ্রিল দ্বিঘাত অন্যোন্যতা (quadratic reciprocity) নিয়মটি প্রমাণ করেন। এই অসাধারণ সাধারণ সূত্রের মাধ্যমে কোন দ্বিঘাত সমীকরণ মডুলার পাটীগণিতের মাধ্যমে সমাধান করা সম্ভব কি না, তা নির্ধারণ করা যায়। ৩১শে মে তারিখে তিনি মৌলিক সংখ্যা উপপাদ্যটি অনুমান করেন, যা মৌলিক সংখ্যার বণ্টন সম্বন্ধে ধারণা প্রদান করে।
গাউস আরও আবিষ্কার করেন যে সকল ধনাত্মক পূর্ণসংখ্যাকে সর্বোচ্চ তিনটি ত্রিভুজীয় সংখ্যা (triangular number) যোগফল হিসেবে প্রকাশ করা যেতে পারে; এই উদ্ভাবনের তারিখটি ছিল ১০ জুলাই এবং এ সম্বন্ধে তার ডায়েরিতে লেখা ছিল সেই বিখ্যাত শব্দগুচ্ছ, "ইউরেকা! num = Δ + Δ + Δ." অক্টোবর 1 তারিখে তিনি সসীম ক্ষেত্র (finite field) সহগবিশিষ্ট বহুপদীর সমাধান সংখ্যার ওপর একটি নিবন্ধ প্রকাশ করেন, যা ১৫০ বছর পর ভেইল অনুমিতির জন্ম দেয়।
মধ্যজীবন (১৭৯৯–১৮৩০)
১৭৯৯ সালে তার ডক্টরেট অভিসন্দর্ভ সকল একক-চলকবিশিষ্ট সমাকলক মূলদ বীজগাণিতিক ফাংশনকে প্রথম বা দ্বিতীয় ঘাতের বাস্তব উৎপাদকের গুণফল আকারে প্রকাশ করার তত্ত্বের একটি নতুন প্রমাণ-এ গাউস বীজগণিতের মৌলিক তত্ত্বটি (fundamental theorem of algebra) প্রমাণ করেন, যা হল জটিল সংখ্যায় সকল অ-ধ্রুবক একক-চলকধারী বহুপদীর কমপক্ষে একটি মূল আছে। তার পূর্বে কিছু গণিতবিদ এ তত্ত্বটির ভুল প্রমাণ দিয়েছিলেন, যাদের মধ্যে ছিলেন জঁ ল্য রোঁ দালঁবের (Jean le Rond d'Alembert)। তবে শ্লেষের ব্যাপার হল এই যে বর্তমান মানদন্ডে গাউসের প্রমাণটিও পুরোপুরি সঠিক নয়, কারণ তিনি জর্ডানের বক্রতা তত্ত্বের (Jordan curve theorem) পরোক্ষ ব্যবহার করেছিলেন। তবে পরবর্তীতে তিনি এ তত্ত্বের তিনটি প্রমাণ উপস্থাপন করেন, যার শেষটি ছিল সাধারণভাবে কড়াকড়ি প্রমাণ। তার প্রচেষ্টা পাশাপাশি জটিল সংখ্যার ধারণাও স্পষ্টতর করে।
গাউস সংখ্যাতত্ত্বেও গুরুত্বপূর্ণ অবদান রাখেন। ১৮০১ সালে প্রকাশিত বই ডিসকিশিয়নেস এরিথমেটিকা (ল্যাটিন, পাটীগণিতে অনুসন্ধান) এ তিনি কনগ্রুয়েন্স বা অনুসমতার জন্যে একটি নতুন চিহ্নের &equiv ব্যবহার প্রচলন করেন এবং এর মাধ্যমে ভাগশেষ পাটীগণিতের পরিষ্কার উপস্থাপনা করেন, দ্বিঘাত অন্যোন্যতা তত্ত্বের প্রথম দুইটি প্রমাণ লিপিবদ্ধ করেন, দ্বিমিক (binary) ও ত্রিমিক (ternary) দ্বিঘাত রূপের তত্ত্ব বর্ণনা করেন, তাদের জন্যে শ্রেণী সংখ্যা সমস্যা (class number problem) উদ্ধৃত করেন, এবং দেখান যে সুষম সপ্তদশভুজ কম্পাস ও দাগ-না-কাটা রুলার দিয়ে অঙ্কণ (Compass and straightedge constructions) করা সম্ভব।
একই বছর ইতালীয় জ্যোতির্বিজ্ঞানী জুসেপ্পে পিয়াৎজি (Giuseppe Piazzi) বামন গ্রহ সেরেস (Ceres) আবিষ্কার করেন, কিন্তু তিনি মাত্র কয়েকদিন গ্রহটি পর্যবেক্ষণ করতে সমর্থ হন। গাউস গ্রহটির অবস্থান সঠিকভাবে হিসাব করে পুনরায় একে খুঁজে পাওয়ার পথ বাতলে দেন, এবং ১৮০১ সালের ৩১শে ডিসেম্বর ফ্রাঞ্জ জাভের ফন জাখ (Franz Xaver von Zach) গোথায় গ্রহটি পুনরাবিষ্কার করেন এবং তার এক দিন পর হাইনরিশ অলবের্স-ও (Heinrich Wilhelm Matthäus Olbers) ব্রেমেনে বসে গ্রহটি খুঁজে পেতে সমর্থ হন।
জাখ মন্তব্য করেন, "ডক্টর গাউসের বুদ্ধিদীপ্ত গণনা ছাড়া আমরা হয়তো গ্রহটি আর খুঁজে পেতাম না।" যদিও তখন পর্যন্ত গাউস ডিউকের কাছ থেকে বৃত্তি পাচ্ছিলেন, তিনি এই ব্যবস্থার নিরাপত্তা নিয়ে শঙ্কিত ছিলেন, তাছাড়া তিনি মনে করতেন বিশুদ্ধ গণিত অর্থনৈতিক সহায়তা লাভ করার মত যথেষ্ট গুরুত্বপূর্ণ নয়। তিনি জ্যোতির্বিজ্ঞানী হিসেবে চাকরি খঁজতে শুরু করেন এবং ১৮০৭ সালে গোটিঙেনের জ্যোতির্বিজ্ঞান পর্যবেক্ষণ কেন্দ্রে জ্যোতির্বিজ্ঞান অধ্যাপক ও পরিচালক হিসেবে নিয়োগ লাভ করেন। জীবনের শেষ দিন পর্যন্ত তিনি এ চাকরিতে বহাল ছিলেন।
১৮০১ সালের ১লা জানুয়ারি পিয়াৎজির সেরেস আবিষ্কার গাউসকে বৃহৎ গ্রহ দ্বারা বাঁধাগ্রস্ত উপগ্রহের গতি নিয়ে কাজ করতে উদ্বুদ্ধ করে, যা ১৮০৯ সালে Theoria motus corporum coelestium in sectionibus conicis solem ambientum ("সূর্যের চারপাশে মহাকাশের বস্তুসমূহের কোণক আকৃতির গতি সম্পর্কিত তত্ত্ব") নামে প্রকাশিত হয়। পিয়াৎজি সেরেসকে কেবলমাত্র কয়েক মাসের জন্য পর্যবেক্ষণ করতে সমর্থ হন, তার সেরেসের পর্যবেক্ষণ রাতের আকাশে তিন ডিগ্রি পর্যন্ত সীমাবদ্ধ ছিল। এরপর গ্রহটি সূর্যের আড়ালে ক্ষণস্থায়ীভাবে ঢাকা পড়ে যায়। কয়েকমাস পরে সেরেসকে যখন পুনরায় দেখতে পাবার কথা, তখন পিয়াৎজি তা খুঁজে পেতে ব্যর্থ হন: সে সময়কার গাণিতিক উৎকর্ষ কেবলমাত্র তিন ডিগ্রি কক্ষপথের হিসাব থেকে প্রকৃত কক্ষপথ হিসাব করবার মতো যথেষ্ট দক্ষ ছিল না— তিন ডিগ্রি প্রকৃত কক্ষপথের ১% এরও কম অংশ।
২৩ বছর বয়সে গাউস এ সমস্যার সাথে পরিচিত হন এবং তা নিয়ে কাজ করতে শুরু করেন। তিন মাসের কঠোর পরিশ্রমের মাধ্যমে তিনি ডিসেম্বর ১৮০১ সালের জন্যে সেরেসের কক্ষপথ ভবিষদ্বাণী করেন— এবং তা এক ডিগ্রির অর্ধেকেরও কম ত্রুটিসহ সঠিক প্রমাণিত হয়। স্বর্গীয় বস্তুসমূহের গতি আজও জ্যোতির্বৈজ্ঞানিক গণনায় মাইলফলক হিসাবে বিবেচিত। এ তত্ত্বে তিনি গাউসীয় মহাকর্ষ ধ্রুবক ধারণাটির জন্ম দেন এবং সর্বনিম্ন বর্গ পদ্ধতি ব্যবহার করেন, যা কিনা আজও বিভিন্ন বৈজ্ঞানিক গবেষণায় ত্রুটি সর্বনিম্নকরণের কাজে ব্যবহৃত হয়। গাউস ১৮০৯ সালে এ তত্ত্বটি স্বাভাবিকভাবে বন্টিত ত্রুটির জন্যে প্রমাণ করতে সমর্থ হন।
গাউস অ-ইউক্লিডীয় জ্যামিতির (non-Euclidean geometry) সম্ভাবনার কথাও আবিষ্কার করেছিলেন বলে দাবি করেন, কিন্তু এ সম্পর্কে তার কোন কাজ তিনি প্রকাশ করেন নি। এ আবিষ্কারটি ছিল গণিতের জগতে একটি যুগান্তকারী পরিবর্তনের সূচনা, কেবলমাত্র ইউক্লিডের স্বতঃসিদ্ধের মাধ্যমেই যুক্তিযুক্ত ও অসঙ্গতিবিহীন জ্যামিতি তৈরি করা যায় - এ ভ্রান্ত ধারণা থেকে গণিতবিদদের মুক্ত করে।
ধরনের জ্যামিতির ওপর গবেষণার মাধ্যমে অনেক নতুন আবিষ্কার হয়, যার মধ্যে অন্যতম হল আইনস্টাইনের সাধারণ আপেক্ষিকতা তত্ত্ব, যা মহাবিশ্বকে অ-ইউক্লিডীয় হিসেবে ব্যাখ্যা করে। গাউসের বন্ধু ফারকাস উলফগ্যাং বোলাই যার সাথে তিনি ছাত্রাবস্থায় ভ্রাতৃত্ব ও সত্যের পতাকার শপথ নিয়েছিলেন, তিনি বহু বছর ধরে ইউক্লিডের অন্যান্য উপপাদ্য ব্যবহার করে সমান্তরাল স্বীকার্যটি প্রমাণ করার ব্যর্থ চেষ্টা করেন। বোলাইয়ের পুত্র জেনোস বোলাই ১৮২৯ সালে অ-ইউক্লিডীয় জ্যামিতি আবিষ্কার করেন; তার কাজ ১৮৩২ সালে প্রকাশিত হয়। তা দেখার পর গাউস ফারকাস বোলাইকে লেখেন: "এর প্রশংসা করা আমার জন্যেও গৌরবের। কারণ কাজটির প্রায় সম্পূর্ণ অংশই.... আমার এ সংক্রান্ত গত তিরিশ বা পয়ত্রিশ বছরের চিন্তা-ভাবনার সাথে মিলে যায়।"
কার্ল ফ্রিডরিখ গাউস ১৭৭৭ সালের ৩০ এপ্রিল জন্মগ্রহণ করেন বর্তমান লোয়ার সাক্সনির অন্তর্গত ব্রাউনশভিগে। তাঁর পিতামাতা ছিলেন নিতান্তই খেটে-খাওয়া শ্রেণীর। শৈশবেই তিনি তাঁর গাণিতিক প্রতিভার পরিচয় দিতে শুরু করেন। তার অসাধারণ প্রতিভা সম্বন্ধে বেশ কিছু গল্প প্রচলিত আছে। কথিত আছে মাত্র তিন বছর বয়সে তিনি তার বাবার হিসাবের খাতার ভুল ধরে দেন মনে মনে গণনা করে। তার সম্বন্ধে আরেকটি বহুল প্রচলিত গল্প হচ্ছে- একবার তার প্রাথমিক বিদ্যালয়ের শিক্ষক দুষ্টু ছাত্রদের ব্যস্ত রাখবার জন্যে ১ থেকে ১০০ পর্যন্ত সংখ্যাগুলো যোগ করতে বলেন। গাউস তার শিক্ষককে অবাক করে দিয়ে মুহুর্তের মধ্যেই সঠিক উত্তরটি বের করে ফেলেন।
গাউসের যোগ করার পদ্ধতিটি ছিল অত্যন্ত সহজ - তিনি লক্ষ্য করেন ধারাটির দুই বিপরীত দিক থেকে পদ নিয়ে জোড়া তৈরি করতে থাকলে তাদের যোগফল সমান থাকে 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, এবং এভাবে সম্পূর্ণ যোগফলটি দাঁড়ায় 50 × 101 = 5050। তবে এই গল্পটির বিস্তারিত বিবরণ কিছুটা অনুমান করা বলেই মনে করা হয়; কিছু লেখক, যেমন জোসেফ রটম্যান তার বই এ ফার্স্ট কোর্স ইন এলজেবরাতে ঘটনাটি আদৌ ঘটেছিল কিনা তা নিয়েই সন্দেহ প্রকাশ করেছেন।
গাউসের বুদ্ধিবৃত্তিক ক্ষমতা ব্রাউনশভিগের ডিউকের নজর কাড়ে, যিনি তাকে কলোজিয়াম কারোলিনামে (বর্তমান টেকনিশে উইনিভার্সিতেত ব্রাউনশভিগ) এ পড়ালেখা করবার সুযোগ করে দেন। তিনি ১৭৯২ থেকে ১৭৯৫ পর্যন্ত সেখানে অধ্যয়ন করেন এবং তারপর গোটিগেন বিশ্ববিদ্যালয়ে ১৭৯৫ থেকে ১৭৯৮ পর্যন্ত পড়েন।

ইতিহাসের সবচেয়ে বড় গণিতবিদদের তালিকায় কার্ল ফ্রেডরিক গাউস উজ্জ্বল এক নাম। তাঁর পরিচয় দেবার আগে একটা ছোট ঘটনা দিয়ে শুরু করি! ছোটবেলায় তিনি ছিলেন খুব অস্থির প্রকৃতির। এজন্য ক্লাসের শিক্ষকদের খুব অসুবিধা হতো। তাই কিশোর গাউসকে ব্যস্ত রাখার জন্য একবার এক শিক্ষক “1+2+3………+100” এর ধারার যোগফল নির্ণয় করতে বললেন। তিনি আশা করেছিলেন যে অনেকগুলো সংখ্যা লিখে যোগ করতে গাউসের বেশ কিছুটা সময় লাগবে। শিক্ষককে ভুল প্রমাণ করেছিলেন গাউস। তিনি লক্ষ করলেন যে ধারাটি একেবারে সোজা – একবার উল্টো দিক থেকে লিখলে প্রতি জোড়া সংখ্যার যোগফল সমান হয়!
S=1+2+3+………+100
S=100+99+98+….+1
2S= 101+101+101+……..+101
or, 2S= 101.100
or, S= 50.101=5050
দুই মিনিটের মাথায় গাউস শিক্ষকের কাছে সমস্যার সমাধান দিয়ে আসলেন। শিক্ষক অবাক হলেন। এ সমস্যার সমাধান করতে গাউসের কমপক্ষে ১০ থেকে ১৫ মিনিট লাগার কথা। নিজের ছাত্রের পদ্ধতি বুঝতে শিক্ষকের পর্যন্ত বেশ সময় লেগেছিলো!
খুব কম বয়সে কার্ল ফ্রেডরিক গাউস এমন মেধারই পরিচয় দিয়েছিলেন। গণিতের খুব কম শাখা আছে যেখানে তাঁর অবদান নেই। সংখ্যা তত্ত্ব, বীজগণিত, পরিসংখ্যান, গাণিতিক বিশ্লেষণ, ডিফারেন্সিয়াল জ্যামিতি, জিওফিজিক্স, স্থির তড়িৎ, জ্যোতির্বিদ্যা, ম্যাট্রিক্স থিওরি ও অপটিক্সে অসামান্য অবদান রেখেছিলেন তিনি।
জীবনের শেষভাগ ও মৃত্যু (১৮৩১–১৮৫৫)
১৮৩১ সালে গাউস পদার্থবিজ্ঞানের অধ্যাপক ভিলহেলম ওয়েবারের সাথে যৌথ গবেষণায় নিযুক্ত হন, যার ফলস্বরূপ চুম্বকত্বে নতুন জ্ঞান (যার মধ্যে রয়েছে ভর, দৈর্ঘ্য ও সময়ের সাপেক্ষে চুম্বকত্ব প্রকাশের একক) এবং তড়িতের কার্শফের বর্তনী সংক্রান্ত সূত্র আবিষ্কৃত হয়। তারা ১৮৩৩ সালে তড়িৎ-যান্ত্রিক টেলিগ্রাফ উদ্ভাবন করেন, যা অবজার্ভেটরির সাথে গোটিগেনের পদার্থবিজ্ঞান ইন্সটিটিউটের সংযোগ সাধন করে। তিনি অবজার্ভেটরির বাগানে একটি চৌম্বক অবজার্ভেটর স্থাপনের আদেশ করেন এবং ওয়েবারের সাথে magnetischer Verein (জার্মান ভাষায় চৌম্বক সভা ) স্থাপন করেন, যা পৃথিবীর বিভিন্ন অঞ্চলে পৃথিবীর চৌম্বক ক্ষেত্রে পরিমাপ কাজকে সহায়তা করে। তিনি চৌম্বক ক্ষেত্রের সমান্তরাল তীব্রতা পরিমাপের একটি পদ্ধতি আবিষ্কার করেন যা ২০ শতকের দ্বিতীয়ার্ধ পর্যন্ত ব্যবহৃত হয় এবং পৃথিবীর চৌম্বক ক্ষেত্রের আভ্যন্তরীন (মজ্জা এবং ত্বক) এবং বহির্গত উৎসের পার্থক্যসূচক গাণিতিক তত্ত্ব প্রতিষ্ঠা করেন।
গাউস ১৮৫৫ সালে গোটিগেনে মৃত্যুবরণ করেন এবং সেখানেই তাকে সমাহিত করা হয়। দু'জন ব্যক্তি তার শেষকৃত্যানুষ্ঠানে প্রশংসাবাক্য পাঠ করেন, গাউসের জামাতা হাইনরিখ এওয়াল্ড এবং উলফগ্যাং সার্টরিয়াস ফন ভালটারশসেন, যিনি ছিলেন গাউসের ঘনিষ্ঠ বন্ধু ও তার জীবনীকার। তার মস্তিষ্ক রুডলফ ভাগনার কর্তৃক সংরক্ষিত ও পর্যবেক্ষিত হয়, যিনি সেটির ভর গণনা করেন ১৪৯২ গ্রাম এবং সেরেব্রাল এলাকা ২,১৯,৫৮৮ বর্গ মিমি।[৭] (৩৪০.৩৬২ বর্গ ইঞ্চি)। সুগঠিত মোচড়ও সেখানে আবিষ্কৃত হয়, যাকে ২০ শতকের গোড়ার দিকে তার অসামান্য প্রতিভার কারণ হিসেবে চিহ্নিত করা হয়েছিল
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0